基本介紹
定義
性質
判定
角平分線定義
角平分線性質
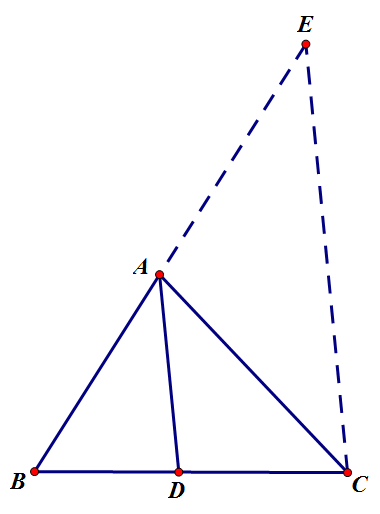
作法
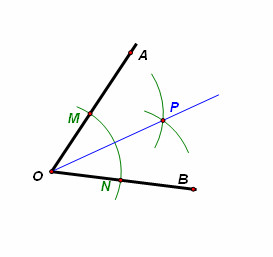 角平分線作法
角平分線作法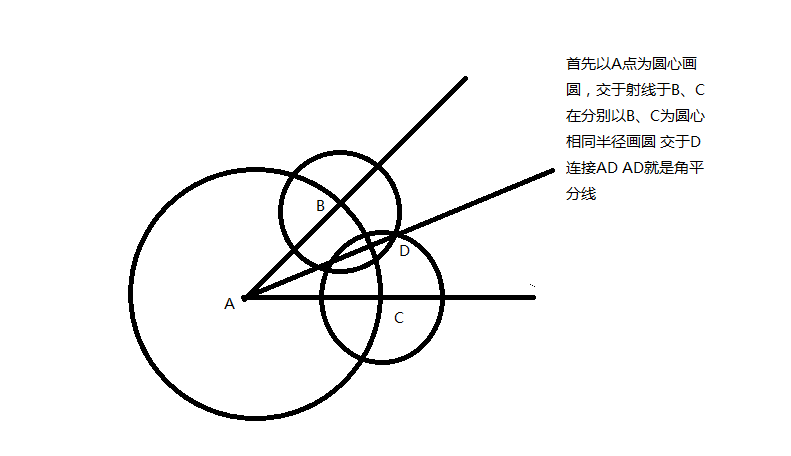

 角平分線作法
角平分線作法角平分線定義(Angle bisector definition)從一個角的頂點引出一條射線,把這個角分成兩個完全相同的角,這條射線叫做這個角的角平分線。三角形三條角平分線的交點...
角平分線定理1是描述角平分線上的點到角兩邊距離定量關係的定理,也可看作是角平分線的性質。角平分線定理2是將角平分線放到三角形中研究得出的線段等比例關係的...
角平分線的性質:1.角平分線可以得到兩個相等的角。2.角平分線上的點到角兩邊的距離相等。3.三角形的三條角平分線交於一點,稱作三角形內心。三角形的內心到...
三角形的角平分線:三角形其中一個內角的平分線與它的對邊相交,這個角的頂點與交點之間的線段叫做三角形的角平分線。...
一般地,從一個角的頂點出發,把這個角分成兩個相等的角的射線,叫做這個角的平分線。(angular bisector)。...
角平分線長公式描述了三角形內角平分線長與各線段間的定量關係。...... 角平分線長公式描述了三角形內角平分線長與各線段間的定量關係。中文名 角平分線長公式 ...
角平分線成比例定理是數學中的一種定理,該定理指出三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。...
平分三角形一個角的射線與這個角的對邊相交,則頂點和交點之間的線段叫三角形的一條角平分線。...
如圖所示,BF,CD,AE分別為正三角形ABC的三條高,中線,角平分線,其交點P即為正三角形ABC的中心。詞條標籤: 科技術語 , 科學 圖集 三角形中線圖冊 V百科往期...
角分角平分線 編輯 從一個角的頂點引出一條射線,把這個角分成兩個完全相同的角,這條射線叫做這個角的角平分線。三角形三條角平分線的交點叫做三角形的內心。...
三角形旁切圓的圓心,簡稱為三角形旁心,它是三角形一個內角的平分線和其他兩個內角的外角平分線的交點;顯然,任何三角形都存在三個旁切圓、三個旁心。
