角平分線成比例定理是數學中的一種定理,該定理指出三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。
基本介紹
- 中文名:角平分線分線段成比例定理
- 類型:定理
- 所屬學科:數學
- 條件是:三角形

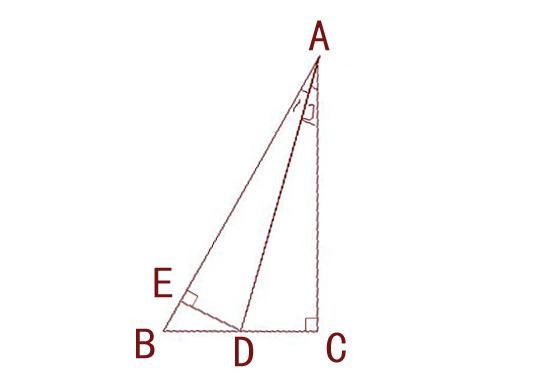
角平分線成比例定理是數學中的一種定理,該定理指出三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。

角平分線成比例定理是數學中的一種定理,該定理指出三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。...
角平分線定理1是描述角平分線上的點到角兩邊距離定量關係的定理,也可看作是角平分線的性質。角平分線定理2是將角平分線放到三角形中研究得出的線段等比例關係的...
角平分線性質定理第四部分 4.三角形一個角的平分線,這個角平分線其對邊所成的兩條線段與這個角的兩鄰邊對應成比例。如右下圖,平面內任意一小於180度的∠MAN,...
內角角平分線定理指的是在角平分線上的點到這個角的兩邊的距離相等, 到一個角的兩邊的距離相等的點,在這個角的平分線上,角的平分線是到角的兩邊距離相等的...
平行線分線段成比例定理指的是兩條直線被一組平行線(不少於3條)所截,截得的對應線段的長度成比例。推論:平行於三角形一邊的直線,截其他兩邊(或兩邊延長線)所...
2.三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。...以上均為國中階段知識點及證法,詳見“角平分線定理”“三角形角平分線”。...
三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。...角的平分線角平分線的定理: 在角平分線上的點到這個角的兩邊的距離相等。...
三角形內角平分線的性質定理:三角形的內角平分線內分對邊成兩條線段,那么這兩條線段與這個角的兩邊對應成比例。三角形內角平分線的判定定理:在Rt△ABC中,若點D...
三角形內角平分線定理:三角形任意兩邊之比等於它們夾角的平分線分對邊之比。...... 分對邊,所得的兩條線段與這個角的兩邊對應成比例.三角形外角平分線的性質定理...
判定定理2:如果兩個三角形的兩組對應邊成比例,並且對應的夾角相等,那么這兩個...2.相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內...
“幾何定理”分類幾何定理條目 編輯 平面幾何:線平行線判定定理平行線性質定理垂直平分線平行線等分線段定理平行線分線段成比例定理角角平分線定理...
26 定理1 在角的平分線上的點到這個角的兩邊的距離相等27 定理2 到一個角...86 平行線分線段成比例定理 三條平行線截兩條直線,所得的對應線段成比例...
定義相似三角形的對應角相等,對應邊成比例。定理相似三角形任意對應線段的比等於...2. 相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內...
