基本介紹
詳細釋義

性質

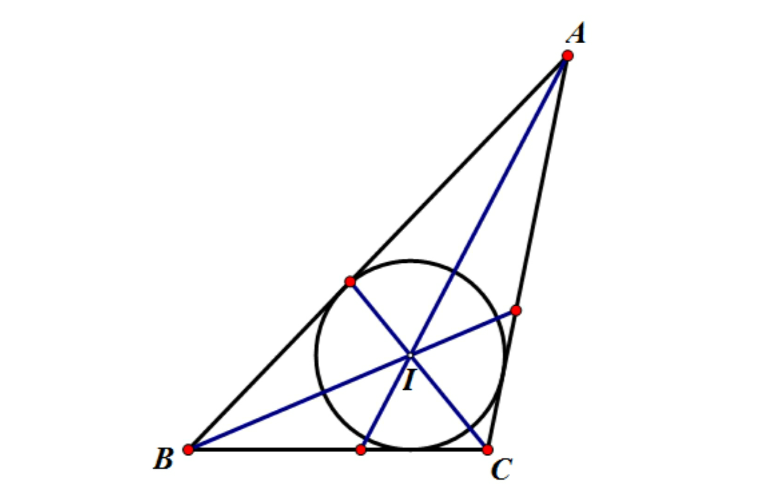


1.謂出於真誠。2.心在體內,故稱為內心。亦指心中、心裡頭。3.三角形內切圓的圓心。4三角形角平分線的交點,到三邊的距離相等
三角形三條內角平分線的交點叫三角形的內心。即內切圓的圓心。內心是三角形角平分線交點的原理:經圓外一點作圓的兩條切線,這一點與圓心的連線平分兩條切線的...
三角形內心指三個內角的三條角平分線相交於一點,這個點叫做三角形的內心。這個點也是這個三角形內切圓的圓心。三角形內心到三角形三條邊的距離相等。...
內心獨白是現代小說,特別是意識流小說的一種重要的表達手法。其特點是用第一人稱直接或用其他人稱間接描寫人物的意識和潛意識活動,以表現人物的內心世界。由於意識...
人生,是一趟沒有回程的旅行,沿途有坎坷泥濘,也有春花秋月。對於旅途中的人來說,精神的豐富和內心的強大才最重要的。內心強大是幫助你積聚外界能量的前提。有了強大...
內心世界是一個漢語詞語,拼音nèi xīn shì ji,是指人的思想感情,思想境界。...... 內心世界是一個漢語詞語,拼音nèi xīn shì ji,是指人的思想感情,思想境界...
悶騷是英語“Man show”的音譯,最早見於中國港澳地區。現逐步成為年輕族群的流行辭彙。悶騷一般是指外表沉悶,內心卻充滿瘋狂。此類人群不輕易表達和外露個人喜怒哀樂...
文化大致可以表述為:1.廣泛的知識並能將之活學活用;2.內心的精神和修養。傳統的觀念認為:文化是人類在社會歷史發展過程中所創造的物質財富 [5] 和精神財富的...
歪歪兔《做內心強大的自己》共有兩部圖畫書。《做內心強大的自己》《做內心強大的自己2》...
三角形的三條內角平分線交於一點。該點叫做三角形的內心。三角形的內心即三角形內切圓的圓心。 內心定理:三角形的三內角平分線交於一點。該點叫做三角形的...
《心內心外》是由Beyond演唱的一首歌曲,出自專輯:《秘密警察》。...... 《心內心外》是由Beyond演唱的一首歌曲,出自專輯:《秘密警察》。中文名稱 心內心外 所...
內心堅強,指人的一種心理素質,也可以指人的胸懷及一種潛力,對未來充滿希望,對人生目標清晰!
《原來占據你內心的人不是我》是賀一航演唱的歌曲,由蔡華壘填詞、孫勇譜曲、艾宇編曲,歌曲發行於2018年8月2日,並收藏在同名專輯《原來占據你內心的人不是我》中...
《淡定:做內心強大的自己》是2013年1月1日中國商業出版社出版的圖書,作者是卡耐基。該書讓讀者重新認知自己,教會讀者學習如何應對複雜多變的生活、控制起伏不定的...
《內心引力》是由施秋榮、胡弦執導,毛繼鴻、Tina、吳永紅等主演的一部創業紀實電影。該片於2017年6月10日在中國大陸上映。該片圍繞“永不違背內心”的主題,通過...
聽從自己內心的安排內容推薦 編輯 每個人都應該做自己喜歡的事,用自己目中無人的喜歡和旁若無人的努力,成為世界的無可替代。 從小,許芳宜就對念書沒有興趣,...
《內心深處》是由伍迪 艾倫執導,傑拉丹·佩姬、黛安·基頓、瑪麗·貝絲·赫特、克里斯汀·格里菲思主演的劇情片,於1978年8月2日在美國上映。該片講述了久未謀面的...
網路流行語。來源於2015年國內漫畫作者陳安妮在接受媒體採訪時說的一句“我的內心幾乎是崩潰的”,被網友們爭相借用。...
【內心分析法】心理描寫技巧之一。用分析人物心理的方法來展示人物內心世界的意識流技巧。傳統小說就已廣泛運用此法來刻畫人物。意識流小說採用並發展了這一手法,...
《淡定:內心強大的力量(最新)》是中國華僑出版社出版的圖書,作者是戴爾·卡耐基。本書介紹了如何應對複雜多變的生活、控制起伏不定的情緒,做一個淡定的強者。...
《做內心強大的自己》是2012年06月01日新世界出版社出版的圖書,作者是卡耐基。...... 《做內心強大的自己》是2012年06月01日新世界出版社出版的圖書,作者是卡耐基...
《我內心深處》是Calary Chen創作的網路小說,發表於晉江文學網。...... 《我內心深處》是Calary Chen創作的網路小說,發表於晉江文學網。中文名稱 我內心深處 作者...
內心信念,是一種內在的、自覺的道德評價行為。指人們依照自己已形成的道德觀念對自己的行為進行自覺的肯定或否定。...
《我喜歡上你時的內心活動》是由韓寒填詞,陳光榮作曲,陳綺貞演唱的歌曲,作為電影《喜歡你》的主題曲於2017年4月10日首發。2018年,該曲先後提名第37屆香港電影金像...
三角形五心是指三角形的重心、外心、內心、垂心、旁心。三條中線的交點是重心,三邊垂直平分線的交點是外心,三條內角平分線的交點為內心,三角形三條高線的交點為...
心理描寫是指在文章中,對人物在一定的環境中的心理狀態、精神面貌和內心活動進行的描寫。是作文中表現人物性格品質的一種方法。最常用的是描寫人物的內心獨白,寫出...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱
自由心證原則要求:對於證據的取捨及其證明力,由法官針對具體案情根據經驗法則、邏輯規則和自己的理性良心自由判斷,由此形成內心確信,並據此認定案件事實。所謂“內心...
