三角形內心指三個內角的三條角平分線相交於一點,這個點叫做三角形的內心。這個點也是這個三角形內切圓的圓心。三角形內心到三角形三條邊的距離相等。
基本介紹
- 中文名:三角形內心
- 定義:三條角平分線的交點
- 套用領域:幾何
- 性質:內心到三角形三條邊的距離相等
共點證明

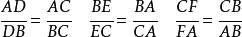
內心性質



內心做法

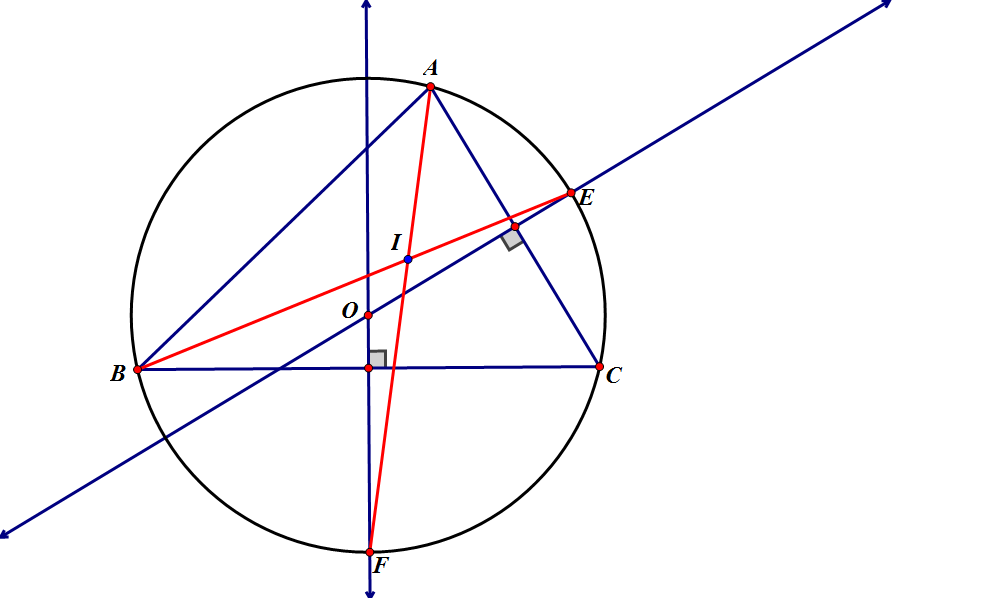
三角形內心指三個內角的三條角平分線相交於一點,這個點叫做三角形的內心。這個點也是這個三角形內切圓的圓心。三角形內心到三角形三條邊的距離相等。

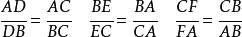




三角形內心指三個內角的三條角平分線相交於一點,這個點叫做三角形的內心。這個點也是這個三角形內切圓的圓心。三角形內心到三角形三條邊的距離相等。...
三角形五心是指三角形的重心、外心、內心、垂心、旁心。三條中線的交點是重心,三邊垂直平分線的交點是外心,三條內角平分線的交點為內心,三角形三條高線的交點為...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱
三角形三條內角平分線的交點叫三角形的內心。即內切圓的圓心。內心是三角形角平分線交點的原理:經圓外一點作圓的兩條切線,這一點與圓心的連線平分兩條切線的...
三角形的四心是指三角形的重心、外心、內心、垂心。若且唯若三角形是正三角形的時候,重心、垂心、內心、外心四心合一心,稱做正三角形的中心。...
三角形的三條內角平分線交於一點。該點叫做三角形的內心。三角形的內心即三角形內切圓的圓心。 內心定理:三角形的三內角平分線交於一點。該點叫做三角形的...
三角形的角平分線:三角形其中一個內角的平分線與它的對邊相交,這個角的頂點與交點之間的線段叫做三角形的角平分線。...
1.謂出於真誠。2.心在體內,故稱為內心。亦指心中、心裡頭。3.三角形內切圓的圓心。4三角形角平分線的交點,到三邊的距離相等
我們知道一個三角形ABC的內心I向三角形三邊作垂線交BC,AC,AB分別於D,E,F(三角形ABC的內切圓切三邊於D,E,F)不難得到AE=AF,BD=BF,CD=CE由塞瓦定理AD,...
與三角形三邊都相切的圓叫做三角形的內切圓,圓心叫做三角形的內心,三角形叫做圓的外切三角形,三角形的內心是三角形三條角平分線的交點。...
三角形的三條高線的交點叫做三角形的垂心。銳角三角形的垂心在三角形內;直角三角形的垂心在直角頂點上;鈍角三角形的垂心在三角形外...
三角形中,連線一個頂點和它所對邊的中點的線段叫做三角形的中線。任何三角形都有三條中線,而且這三條中線都在三角形的內部,並交於一點。由定義可知,三角形的...
給定△ABC及其平面上不在三角形邊上的一點P,聯結AP,BP,CP交對應邊於A',B',C',則△A'B'C'稱為P點關於△ABC的切瓦三角形(Cevian Triangle)。...
三角形三邊關係是三角形三條邊關係的定則,具體內容是在一個三角形中,任意兩邊之和大於第三邊,任意兩邊之差小於第三邊。
三角形元素(elements of triangle)是三角學的基本概念之一,三角形的三邊(或它們的長度)和三內角(或它們的大小)以及由它們所確定的幾何圖形(或相應的幾何量)統稱...
