塞瓦定理是指在△ABC內任取一點O,延長AO、BO、CO分別交對邊於D、E、F,則 (BD/DC)×(CE/EA)×(AF/FB)=1。
塞瓦(Giovanni Ceva,1648~1734)義大利水利工程師,數學家。塞瓦定理載於塞瓦於1678年發表的《直線論》一書,也有書中說塞瓦定理是塞瓦重大發現。
塞瓦定理記憶法:三頂點選一個作為起點,定一方向,繞一圈,三組比例相乘為1。
基本介紹
驗證推導
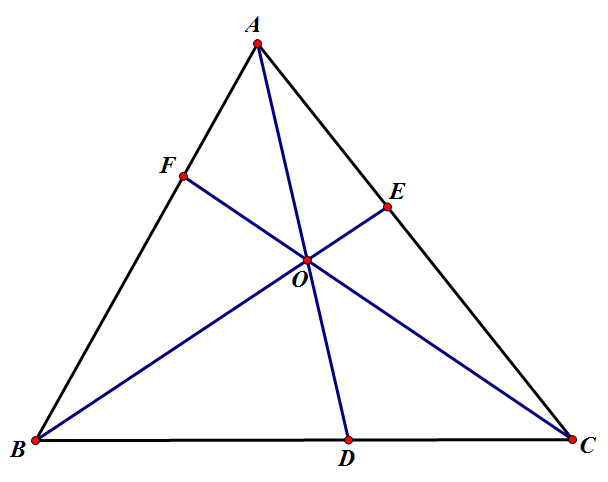

定理推廣


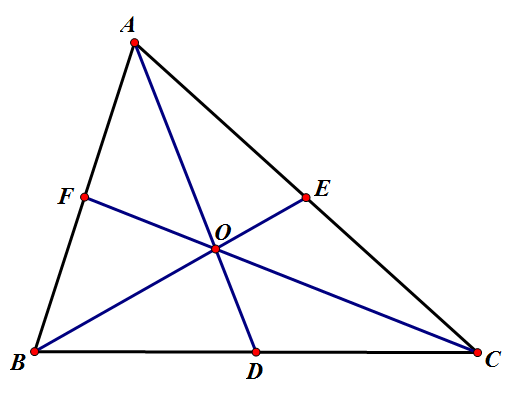 塞瓦定理證明三條中線交於一點
塞瓦定理證明三條中線交於一點數學意義
記憶方法

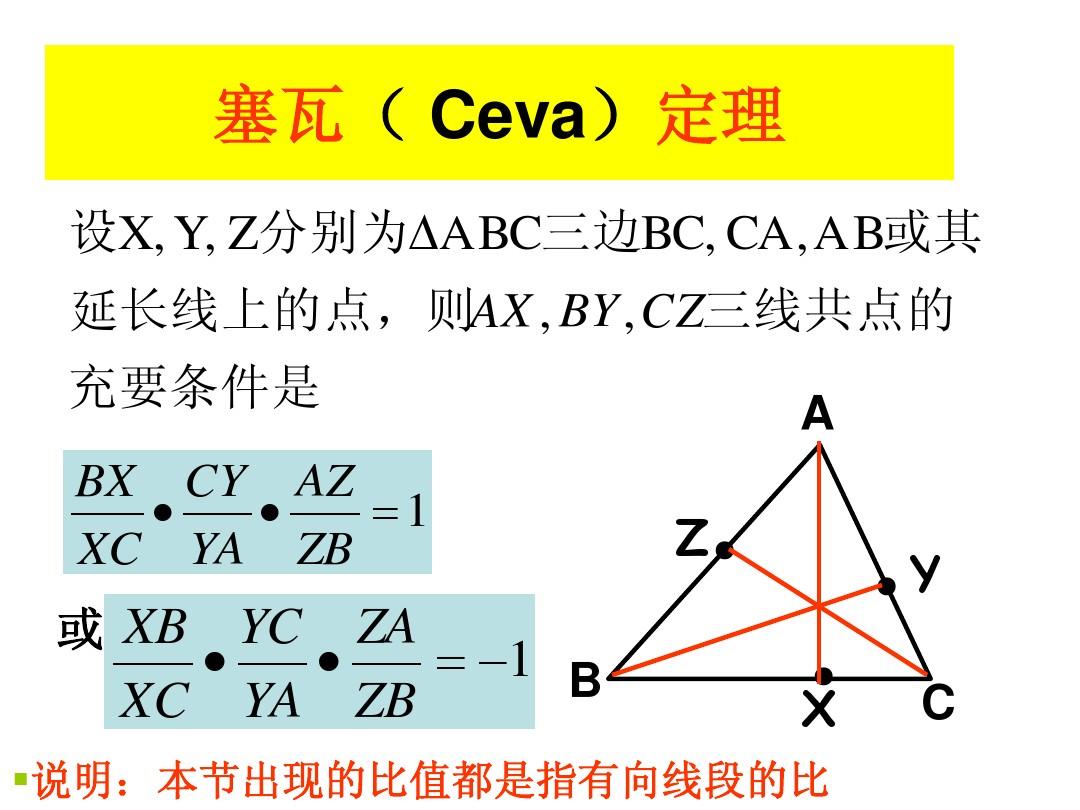
塞瓦定理是指在△ABC內任取一點O,延長AO、BO、CO分別交對邊於D、E、F,則 (BD/DC)×(CE/EA)×(AF/FB)=1。
塞瓦(Giovanni Ceva,1648~1734)義大利水利工程師,數學家。塞瓦定理載於塞瓦於1678年發表的《直線論》一書,也有書中說塞瓦定理是塞瓦重大發現。
塞瓦定理記憶法:三頂點選一個作為起點,定一方向,繞一圈,三組比例相乘為1。




 塞瓦定理證明三條中線交於一點
塞瓦定理證明三條中線交於一點
塞瓦定理是指在△ABC內任取一點O,延長AO、BO、CO分別交對邊於D、E、F,則 (BD/DC)×(CE/EA)×(AF/FB)=1。塞瓦(Giovanni Ceva,1648~1734)義大利水利...
坎德定理是對圓內接四邊形構造射線、切線等操作後後對幾何及代數性質的研究,它與圓冪、根軸、調和聯繫密切,並且近年在高中數學聯賽及以上級別考試考察力度加大。...
梅涅勞斯(Menelaus)定理(簡稱梅氏定理)最早出現在由古希臘數學家梅涅勞斯的著作《球面學》(Sphaerica)中。1任何一條直線截三角形的各邊或其延長線,都使得三條不...
帕斯卡定理指圓錐曲線內接六邊形(包括退化的六邊形)其三對邊的交點共線,與布列安桑定理對偶,是帕普斯定理的推廣。 定理約於公元1639年為法國數學家布萊士·帕斯卡(...
梅涅勞斯逆定理是若有三點F、D、E分別在邊三角形的三邊AB、BC、CA或其延長線上,且滿足AF/FB×BD/DC×CE/EA=1,則F、D、E三點共線。利用這個逆定理,可以...
設D、E、F、分別是三角形ABC的三邊AB、BC、CA、或其延長線上的點,若(BD/CD)*(CE/EA)*(AF/FB)=1.則D、E、F三點共線。梅涅勞斯逆定理常用來證明三點...
三弦共點定理是射影幾何的一個基本定理,卻曾被民間數學家多次"發現"並"命名"。三弦共點定理指出:在圓O中,若弦AB、CD、EF相交於一點P則有:(AC/CF)*(FB/...
喬瓦尼·塞瓦(Giovanni Ceva)(1647年12月7日-1734年6月15日),義大利幾何學家。他發現了綜合幾何上的塞瓦定理。此外,他又重新發現梅涅勞斯定理。...
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。...
數學定理列表(按字母順序排列)以下列出了許多數學定理,供查閱與引用。...... 以下列出了許多數學定理,供查閱與引用。中文...塞瓦定理射影定理三代角定理盛金公式 斯...
數學上的重心是指三角形的三條中線的交點,其證明定理有燕尾定理或塞瓦定理,套用定理有梅涅勞斯定理、塞瓦定理。...
