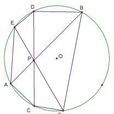
三弦共點定理是射影幾何的一個基本定理,卻曾被民間數學家多次"發現"並"命名"。三弦共點定理指出:在圓O中,若弦AB、CD、EF相交於一點P則有:(AC/CF)*(FB/BD)*(DE/EA)=1。
基本介紹
- 中文名:三弦共點定理
- 類別:幾何定理
- 發現者:民間數學家
簡介,證明方式,逆定理,相似定理,
簡介
設A,B,C,D,E,F是一圓上六點,AD,BE,CF共點的充要條件是: 。
。

證明方式
圓中易得三對相似三角形,
△ACP∽△DBP → AC/DB=PA/PD (1)
△FBP∽△AEP → FB/EA=PF/PA (2)
△EDP∽△CFP → DE/CF=PD/PF (3)
(1)*(2)*(3)得(AC/CF)*(FB/BD)*(DE/EA)=1。
逆定理
若AB、CD、EF是圓O的三條弦,且滿足(AC/CF)*(FB/BD)*(DE/EA)=1,則弦AB、CD、EF交於一點。
相似定理
塞瓦定理:
塞瓦定理是指在△ABC內任取一點O,延長AO、BO、CO分別交對邊於D、E、F,則 (BD/DC)×(CE/EA)×(AF/FB)=1。
塞瓦(Giovanni Ceva,1648~1734)義大利水利工程師,數學家。塞瓦定理載於塞瓦於1678年發表的《直線論》一書,也有書中說塞瓦定理是塞瓦重大發現。
塞瓦定理記憶法:三頂點選一個作為起點,定一方向,繞一圈,三組比例相乘為1。