基本介紹
- 中文名:帕斯卡定理
- 外文名:Pascal's theorem
- 表達式:BG∩EH=Q∈PR
- 提出者:帕斯卡
- 提出時間:公元1639年
- 套用學科:數學
- 適用領域範圍:射影幾何
定理定義
驗證推導
證法1
 面積法
面積法


證法2
 梅涅勞斯定理證法
梅涅勞斯定理證法

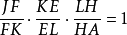




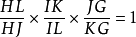
證法3
 位似證法
位似證法證法4

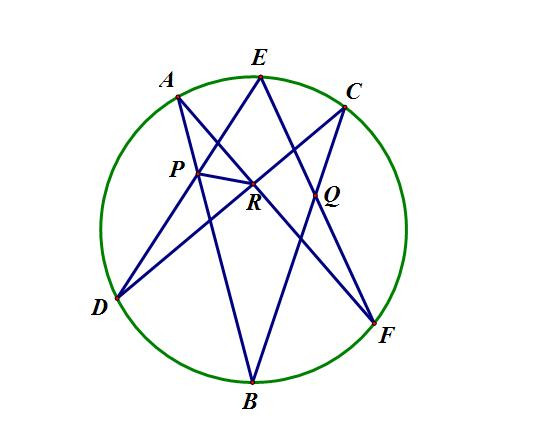 塞瓦定理(角元)證法
塞瓦定理(角元)證法證法5
 射影證法
射影證法
 面積法
面積法


 梅涅勞斯定理證法
梅涅勞斯定理證法

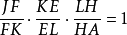




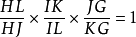
 位似證法
位似證法
 塞瓦定理(角元)證法
塞瓦定理(角元)證法 射影證法
射影證法流體靜力學的一條定律,它指出,不可壓縮靜止流體中任一點受外力產生壓力增值後,此壓力增值瞬時間傳至靜止流體各點。中文名 帕斯卡定律 外文名 Pascal's law ...
帕斯卡定理指圓錐曲線內接六邊形(包括退化的六邊形)其三對邊的交點共線,與布列安桑定理對偶,是帕普斯定理的推廣。 定理約於公元1639年為法國數學家布萊士·帕斯卡(...
布列安桑(Brianchon)定理是一個射影幾何中的著名定理,它斷言六條邊和一條圓錐曲線相切的六邊形的三條對角線共點,此點被稱為該六邊形的布列安桑點。...
特納定理是關於共線點的一個定理。若P,Q是關於△ABC外接圓的一對反演點,點P關於BC,CA,AB三邊的對稱點分別為U,V,W,且QU,QV,QW和邊BC,CA,AB或其延長線...
布萊士·帕斯卡(Blaise Pascal )公元1623年6月19日出生於多姆山省奧弗涅地區的克萊蒙費朗,法國數學家、物理學家、哲學家、散文家。16歲時發現著名的帕斯卡六邊形...
蝴蝶定理(Butterfly Theorem),是古代歐氏平面幾何中最精彩的結果之一。這個命題最早出現在1815年,由W.G.霍納提出證明。而“蝴蝶定理”這個名稱最早出現在《美國數學...
布萊茲·帕斯卡(Blaise Pascal,1623年6月19日-1662年8月19日),法國數學家、物理學家、宗教哲學家。帕斯卡早期進行自然和套用科學的研究,對機械計算器的製造和流體...
布里昂雄定理(Brianchon theorem)是射影幾何的著名定理之一,外切於一個非退化二級曲線的簡單六線形的三對對頂點的連線共點,此點稱為布里昂雄點。此定理是布...
1635年左右開始數學發生興趣,1639年隨父親參加巴黎數學和物理學的學術活動,1640年提出了射影幾何中的帕斯卡定理。 1642~1644年,他設計並創製了歷史上第一架機械計...
《帕斯卡爾的思想哲學》是2008-9-1內蒙文化出版社出版的圖書,作者是劉燁 。...幾何學上的帕斯卡爾六邊形定理,帕斯卡爾三角形,物理學上的帕斯卡爾定理等均是他的...
《牛頓力學及其物理定律:科海拾貝》是2007年1月1日中國標準出版社出版的圖書。...帕斯卡定律液壓機的工作原理液體的壓強液體壓強的公式連通器船閘大氣的壓強大氣壓...
在液體容器底、內壁、內部中,由液體本身的重力而形成的壓強稱為液體壓強,簡稱液壓。帕斯卡“桶裂”實驗可以很好地證明液體壓強與液體的深度有關,因為液體的壓強等於...
兆帕是壓強的單位,全稱為兆帕斯卡。1Pa是指1N的力均勻的壓在1m²面積上所產生的壓強,1兆帕=1000000帕,也可以寫成1MPa=1000000Pa。...
希爾伯特模式(Hilbert mode)亦稱希爾伯特機械化定理.論證幾何問題的一種模式.它出現於希爾伯特(Hilbert , D.)的名著《幾何基礎》第六章之末.原敘述為:“設一種...
上述性質可以推演出許多射影幾何中有關三點共線(或三線共點)的定理, 如帕斯卡定理、帕普斯定理等等,均可簡易證出。相關人物(2張) 特別的,過一個3x3“籠子”...
物體所受的壓力與受力面積之比叫做壓強,壓強用來比較壓力產生的效果,壓強越大,壓力的作用效果越明顯。壓強的計算公式是:p=F/S,壓強的單位是帕斯卡,符號是Pa。...
《思想錄》是17世紀法國數理科學家、思想家布萊茲·帕斯卡爾創作的哲理散文集,...帕斯卡爾自幼就表現出過人的才能,16歲寫成《圓錐曲線論》,其中論證的幾何學定理...
