基本介紹
- 中文名:帕普斯定理
- 外文名:Pappus's theorem
- 提出者:帕普斯
- 套用學科:數學
- 適用領域範圍:計算機, 繪圖,幾何
- 適用領域範圍:射影幾何
定理定義,驗證推導,對偶命題,定理推廣,
定理定義
帕普斯(Pappus)定理:如圖,直線l1上依次有點A,B,C,直線l2上依次有點D,E,F,設AE,BD交於P,AF,DC交於Q,BF,EC交於R,則P,Q,R共線。
驗證推導
證明方法1 證明方法1
證明方法1
 證明方法1
證明方法1(證明過程見右圖)
證明方法2
利用布列安桑定理及其逆定理證明:
如圖,一直線上三點A、B、C,另一直線上三點D、E、F,AE∩BD=M,AF∩DC=N,BF∩EC=O 證明方法2
證明方法2
 證明方法2
證明方法2延長MO至P,由布列安桑逆定理知六邊形PCBMEF內切圓錐曲線,由凹六邊形AMDFPC及其內切圓錐曲線的布列安桑定理知對角線AF∩DC∩MP=N,則M、N、O共線,帕普斯定理得證。
對偶命題
由兩點A,B各出發三條射線,A1,A2,A3;B1,B2,B3,設過A1,B2交點;A2,B1交點的直線為C1,過A2,B3交點;A3,B2交點的直線為C2,過A1,B3交點;A3,B1交點的直線為C3,則C1,C2,C3共點。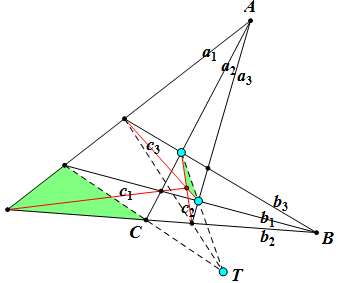

該對偶命題仍然可以利用帕普斯定理(幾何變換形態)及笛沙格定理(逆)證明
此定理在圓中依然成立,圓中以任一直徑為界線,直徑兩側分別取A1,A2,A3;B1,B2,B3。連線A1,B2;A1,B3。A2,B1;A2,B3。A3,B1;A3,B2.則A1B2,A2B1交於C1;A1B3,A3B1交於C2;A2B3,A3B2交於C3。且C1,C2,C3共線。
該對偶命題是布利安桑定理的特例。

