三角形的內切圓

與三角形三邊都相切的圓叫做三角形的內切圓，圓心叫做三角形的內心，三角形叫做圓的外切三角形，三角形的內心是三角形三條角平分線的交點。

基本介紹

• 中文名：三角形的內切圓
• 外文名：inscribed circle of a triangle
• 適用領域範圍：數學
• 適用領域範圍：數學
• 定義：與三角形三邊都相切的圓

概念

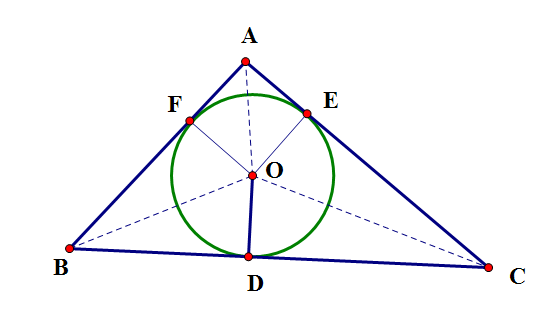
三角形一定有內切圓，其他的圖形不一定有內切圓（一般情況下，n邊形無內切圓，但也有例外，如對邊之和相等的四邊形有內切圓。），且內切圓圓心定在三角形內部。

在三角形中，三個角的角平分線的交點是內切圓的圓心，圓心到三角形各個邊的垂線段相等。

內切圓的半徑為r=2S/C，當中S表示三角形的面積，C表示三角形的周長。

面積法；1/2lr(l周長）用於任意三角形

推論

以內切圓和三角形的三個切點為頂點的三角形A'B'C'是ABC的內接三角形之一。

名稱	確定方法	性質
外心（三角形外接圓的圓心）	三角形三邊中垂線的交點	<1>到三個頂點的距離相等; <2>外心不一定在三角形內部
內心（三角形內切圓的圓心）	三角形三條角平分線的交點	<1>到三邊的距離相等; <2>內心在三角形內部

ABC的內切圓就是A'B'C'的外接圓。而A'A、B'B和C'C三線交於一點，它們的交點就是勒莫恩點（Lemoine point）（或稱熱爾崗點（Gergonne point）），或類似重心，即三條類似中線的交點。內切圓與九點圓相切，切點稱作費爾巴哈點（見九點圓）。

若以三角形的內切圓為反演圓進行反演，則三角形的三條邊和外接圓會分別變為半徑相等的四個圓（半徑都等於內切圓半徑的一半）。

三角形的外接圓半徑R、內切圓半徑r以及內外心間距OI之間有如下關係：

r^2+OI^2= (R-r)^2

在直角三角形的內切圓中，有這樣兩個簡便公式：1、兩直角邊相加的和減去斜邊後除以2，得數是內切圓的半徑。2、兩直角邊乘積除以直角三角形周長，得數是內切圓的半徑。

　1、r=(a+b-c)/2（註：r是Rt△內切圓的半徑，a, b是Rt△的2個直角邊，c是斜邊）

　2、r=ab/ (a+b+c)