三角形二次元素是三角學的基本概念之一,指與三角形有關的圖形面積,如三角形的面積、外接圓的面積及內切圓的面積等。為了提高三角形線性元素的精度,可以通過在其上增加節點並相應地提高插值多項式的次數的辦法,構造三角形二次元素、三角形三次元素等。
基本介紹
- 中文名:三角形二次元素
- 外文名:elements of degree 2 of a triangle
- 適用範圍:數理科學
簡介,計算公式,三角形面積,三角形外接圓的面積,三角形內切圓的面積,套用,
簡介
三角形二次元素是三角學的基本概念之一,指與三角形有關的圖形面積,如三角形的面積、外接圓的面積及內切圓的面積等。
計算公式
三角形面積
1.已知三角形底a,高h,則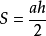 。
。
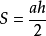
2.(海倫公式)已知三角形三邊a,b,c,則
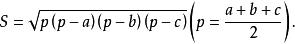
3.已知三角形兩邊a,b,這兩邊夾角C,則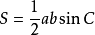 ,即兩夾邊之積乘夾角的正弦值。
,即兩夾邊之積乘夾角的正弦值。
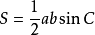
4.設三角形三邊分別為a、b、c,內切圓半徑為r,則三角形面積= 。
。

5.設三角形三邊分別為a、b、c,外接圓半徑為R,則三角形面積= 。
。

6.行列式形式: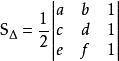 為三階行列式,此
為三階行列式,此 在平面直角坐標系內
在平面直角坐標系內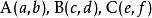 ,這裡
,這裡 選取最好按逆時針順序從右上角開始取,因為這樣取得出的結果一般都為正值,如果不按這個規則取,可能會得到負值,但不要緊,只要取絕對值就可以了,不會影響三角形面積的大小。該公式的證明可以藉助“兩夾邊之積乘夾角的正弦值”的面積公式。
選取最好按逆時針順序從右上角開始取,因為這樣取得出的結果一般都為正值,如果不按這個規則取,可能會得到負值,但不要緊,只要取絕對值就可以了,不會影響三角形面積的大小。該公式的證明可以藉助“兩夾邊之積乘夾角的正弦值”的面積公式。
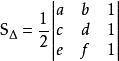

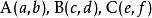

7.海倫——秦九韶三角形中線面積公式:(其中Ma,Mb,Mc為三角形的中線長。)

8.根據向量求面積:

三角形外接圓的面積
由正弦定理可得 ,其中R為外接圓半徑,已知外接圓半徑易得外接圓面積。
,其中R為外接圓半徑,已知外接圓半徑易得外接圓面積。

三角形內切圓的面積
直角三角形的內切圓半徑 (其中a,b為直角邊,c為斜邊),已知內切圓半徑易得內切圓面積。
(其中a,b為直角邊,c為斜邊),已知內切圓半徑易得內切圓面積。

一般三角形的內切圓半徑為 ,S是三角形的面積公式,已知內切圓半徑易得內切圓面積。
,S是三角形的面積公式,已知內切圓半徑易得內切圓面積。

套用
為了提高三角形線性元素的精度,可以通過在其上增加節點並相應地提高插值多項式的次數的辦法,構造三角形二次元素、三角形三次元素等。
