基本介紹
定義
尺規做法
性質



判定方法
相關公式



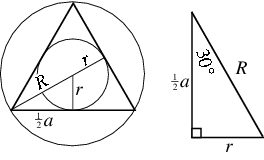 邊長關係
邊長關係











 邊長關係
邊長關係




等邊三角形(又稱正三邊形),為三邊相等的三角形,其三個內角相等,均為60°,它是銳角三角形的一種。等邊三角形也是最穩定的結構。等邊三角形是特殊的等腰三角形...
三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。常見的三角形按邊分有普通三角形(三條邊都不相等),...
一定數目的點或圓在等距離的排列下可以形成一個等邊三角形,這樣的數被稱為三角形數。古希臘著名科學家畢達哥拉斯把數1,3,6,10,15,21……這些數量的(石子),...
拉格朗日點中位於兩較大質量的質點相互繞轉平面上並與它們構成等邊三角形。...... 拉格朗日點中位於兩較大質量的質點相互繞轉平面上並與它們構成等邊三角形。...
任意三角形是一個擁有隨意性的三角形,可以是直角三角形,也可以是銳角三角形,更可以是鈍角三角形、等邊三角形、等腰三角形。...
在三角形中,連線一個頂點和它所對邊的中點的線段叫做三角形的中線。任何三角形都有三條中線,而且這三條中線都在三角形的內部,並交於一點。由定義可知,三角形...
三角形重心是三角形三條中線的交點。當幾何體為勻質物體時,重心與形心重合。...... 3、重心到三角形3個頂點距離平方的和最小。 (等邊三角形)證法一:...
三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。常見的三角形按邊分有普通三角形(三條邊都不相等),...
魯洛克斯三角形(Reuleaux triangle)又稱“勒洛三角形”、“萊洛三角形”、“圓弧三角形”,是一種特殊三角形,指分別以正三角形的頂點為圓心,以其邊長為半徑作圓弧...
三角形圖表是一種較特殊的坐標統計圖方法。它是依據等邊三角形中任意點到三條邊的垂直距離之和相等的原理構成三軸統計圖。因此,專用於內部組成為三項結構的數據...
報備機構:江蘇維納文化傳媒有限公司 2015 年3 月 許可證號: (蘇)字第00691號 劇名題材 體裁 集數 拍攝日期 製作周期 一般 喜劇 戲曲 愛情等邊三角形 當代都市...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱
謝爾賓斯基三角形(英語:Sierpinski triangle)是一種分形,由波蘭數學家謝爾賓斯基在1915年提出。它是自相似集的例子。它的豪斯多夫維是log(3)/log(2) ≈ 1.585。...
三角形面積公式是指使用算式計算出三角形的面積,同一平面內,且不在同一直線的三條線段首尾順次相接所組成的封閉圖形叫做三角形,符號為△。常見的三角形按邊分有...
這種臉型是額頭比較窄,臉的最寬處是下頜,呈現上小下大的正三角形,在視覺上是最有穩定性的一種臉型。洋梨型臉能給人親切、溫和、不拘小節的感覺,同時也顯得臉...
正三稜錐是錐體中底面是正三角形,三個側面是全等的等腰三角形的三稜錐。正三稜錐不等同於正四面體,正四面體必須每個面都是全等的等邊三角形。...
