魯洛克斯三角形(Reuleaux triangle)又稱“勒洛三角形”、“萊洛三角形”、“圓弧三角形”,是一種特殊三角形,指分別以正三角形的頂點為圓心,以其邊長為半徑作圓弧,由這三段圓弧組成的曲邊三角形稱為魯洛克斯三角形。魯洛克斯三角形的特點是:在任何方向上都有相同的寬度,即能在距離等於其圓弧半徑a(等於正三角形的邊長)的兩條平行線間自由轉動,並且始終保持與兩直線都接觸。機械加工業上利用這個性質,把鑽頭的橫截面做成魯洛克斯三角形的形狀,就能在零件上鑽出正方形的孔來,這一性質是魯洛克斯(F.Reuleaux)在研究機械分類時發現的。
基本介紹
- 中文名:魯洛克斯三角形
- 外文名:Reuleaux triangle
- 別稱:勒洛(萊洛)三角形,圓弧三角形
- 所屬學科:數學
- 所屬問題:平面幾何(三角形)
基本介紹,Reuleaux三角形的性質,Reuleaux三角形的套用,
基本介紹
“魯洛克斯三角形”是這樣得到的:先畫正三角ABC,然後以正三角形ABC的三個頂點為圓心,邊長長為半徑畫弧得到的圖形,如圖1。
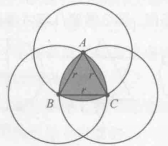 圖1(a)
圖1(a) 圖1(b)
圖1(b)等寬曲線
圓和圓弧三角形具有這樣一個特徵:不論從什麼方向用兩條平行線去夾逼它,這兩條平行線間的距離總是一樣的。我們稱具有這種性質的圖形叫做“等寬曲線”(或定寬圖形)。
等寬曲線最初的定義由一個十九世紀的德國工程師Franz Reuleaux給出的:將一一個曲線圖放在兩條平行線中間,使之與這兩平行線相切,無論這個曲線圖如何運動,只要它還是在這兩條平行線內,就始終與這兩條平行線相切。這兩條平行線間的距離稱為等寬曲線的寬度。
圓弧三角形又叫萊洛三角形、魯洛克斯三角形,是由機械學家、數學家萊洛首先發現的,故而得名。
Reuleaux三角形的性質
邊長為a的魯洛克斯三角形的寬度為a,直徑為a的圓的寬度也為a,同寬度的魯洛克斯三角形與圓具有一些相同的性質:
(1)顯然,作為寬度為a的等寬曲線,魯洛克斯三角形或圓上任意兩點間的距離不會超過a。
(2)將它們放在一個邊長為a的正方形內旋轉時,都能夠始終保持與正方形的每一邊都有且只有一個公共點,且兩對邊的公共點的連線互相垂直。
(3)它們有相同的周長。
邊長為a的魯洛克斯三角形的周長為 ,直徑為a的圓的周長為
,直徑為a的圓的周長為 。
。


Reuleaux三角形的套用
常見的鑽頭鑽出的孔都是圓形的,那有沒有可能鑽出的方形的孔呢?
由於魯洛克斯三角形在一個邊長為其寬度的正方形內轉動時,任何時候都有四個點與正方形的四條邊接觸(不一定相切)且接觸點的位置是不斷改變的(如圖2所示),因而成了機,械學家萊洛設計方孔鑽頭靈感的來源,而促使他發現了圓弧三角形和造出了方孔鑽頭。
當然,這種圓弧三角形的鑽頭鑽出來的不是標準的正方形,而是如圖2(c)所示的圓角正方形。因為魯洛克斯三角形的中心即為正三角形的中心(三條中線的交點),所以,當萊洛三角形鑽頭轉動時,它的中心也不像圓孔鑽那樣固定不變。
魯洛克斯三角形這一特性,也被用於汪克爾(Wankd)發動機,在這種發動機中,魯洛克斯三角形的活塞就在正方形封閉體內旋轉。馬自達(Mazda)汽車發動機就是這樣,當萊洛三角形轉子轉動的時候,轉子邊緣與轉子殼體內壁之間會形成容積呈周期性平滑變化的3個工作室。
魯洛克斯三角形曾上過高考卷,2011年高考數學江西卷(文)第10題:如圖,一個“凸輪”放置於直角坐標系x軸上方,其“底端”落在原點O處,一頂點及中心M在y軸正半軸上,它的外圍由以正三角形的頂點為圓心,以正三角形的邊長為半徑的三段等弧組成。
 圖3
圖3今使“凸輪”沿x軸正向滾動前進,在滾動過程中“凸輪”每時每刻都有一個“最高點”,其中心也在不斷移動位置,則在“凸輪”滾動一周的過程中,將其“最高點”和“中心點”所形成的圖形按上、下放置,應大致為( )。
 圖4
圖4答案:A。
解析:中心M點到x軸的距離按照增大、減小、增大、減小、.....的規律變化,最高點到x軸的距離一直為圓的半徑,所以選A。
由魯洛克斯三角形的啟發,可知還有更多的等寬曲線。如以正五邊形ABCDE的五個頂點為圓心,以對角線AC=a之長為半徑畫五段圓弧,就可以作出一個圓弧五邊形,它便是一個寬度為a的等寬曲線(如圖5所示)。類似地,還可作出圓弧七邊形、圓弧九邊形...得到各種“萊洛多邊形”,它們都是等寬曲線。
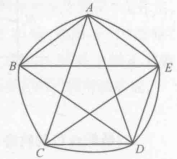 圖5
圖5 圖6
圖6但是,如果您想用邊數為偶數的正多邊形作出一條等寬曲線,已被證明是不可能的。
上面所說的都是正多邊形組成的等寬曲線,其實,只需對角線相等而邊長不一定相等的奇數邊多邊形,都可形成等寬曲線(如圖6)。
可以看出,上面作出的圓弧多邊形都有尖角(在兩條弧的交點處),是否可以將尖角清除,讓它光滑一些呢?
事實上,以萊洛三角形為例,只需經過如下的“處理”,就可以作出與其相應沒有任何尖角頂的光滑的新的等寬曲線。
方法一 把等邊三角形的各邊向兩個方向 延長相等的一段;以三個頂點為圓心畫圓弧,使得三個內角所對的圓弧的半徑,等於邊長與延長線的長度的和;內角的對頂角所對的圓弧,等於延長線的長。由這樣的六條圓弧組成的等寬曲線克服了尖點,因此光滑得多了,如圖7(a)所示(圖7(b)為五邊形等寬曲線圖形)。
 圖7(a)
圖7(a) 圖7(b)
圖7(b)方法二 找到等邊三角形的外接圓圓心,分別連線外心與三角形的三個頂點。取三條線段中點,以這三點為圓心,以二分之一線段長為半徑畫圓,內部圓弧與外部圓弧的交點間的內部圓弧即可克服魯洛克斯三角形的尖點。
值得注意的是,等寬曲線不只限於圓弧等寬曲線,人們已發現了完全不包含圓弧的等寬曲線,那是一類特殊的卵形曲線。因此我們可以說等寬曲線還有許多離奇奧妙的性質和用途等待我們去探究。

