基本介紹
- 中文名:弦長公式
- 類型:概念,公式
- 類別:定理
- 套用學科:數學
公式一
引入
 弦長公式
弦長公式證明




















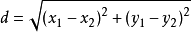
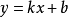

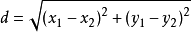





公式二

 拋物線
拋物線


公式三






 弦長公式
弦長公式



















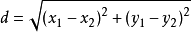
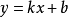

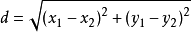






 拋物線
拋物線







弦長公式,在這裡指直線與圓錐曲線相交所得弦長d的公式。PS:圓錐曲線, 是數學、幾何學中通過平切圓錐(嚴格為一個正圓錐面和一個平面完整相切)得到的一些曲線,如:...
弧長計算公式是一個數學公式,為L=n× π× r/180,L=α× r。其中n是圓心角度數,r是半徑,L是圓心角弧長。...
前後緣的距離稱為弦長。如果機翼平面形狀不是長方形,一般在參數計算時採用製造商指定位置的弦長或平均弦長...
扇形計算公式編輯 鎖定 討論999 一條弧和經過這條弧兩端的兩條半徑所圍成的圖形叫扇形(半圓與直徑的組合也是扇形)。顯然, 它是由圓周的一部分與它所對應的圓心...
弧長公式是平面幾何的基本公式之一。弧長公式敘述了弧長,即在圓上過兩點的一段弧的長度,與半徑和圓心角的關係。公式為:l=πrα/180...
兩點間距離公式常用於函式圖形內求兩點之間距離、求點的坐標的基本公式,是距離公式之一。兩點間距離公式敘述了點和點之間距離的關係。...
公式六: 及 與 的三角函式值之間的關係:記背訣竅:奇變偶不變,符號看象限 [2] .即形如(2k+1)90°±α,則函式名稱變為余名函式,正弦變餘弦,餘弦變正弦,...
橢圓面積公式:S=π(圓周率)×a×b,其中a、b分別是橢圓的半長軸,半短軸的長。橢圓面積公式屬於幾何數學領域。...
面積公式是數學公式,其中包括 扇形面積公式,圓形面積公式,弓形面積公式,菱形面積公式,三角形面積公式,梯形面積公式等多種圖形的面積公式。...
本文介紹一個公式,可以簡捷準確地求出直線被拋物線截得的弦長,還可以利用它來判斷直線與拋物線位置關係及解決一些與弦長有關的題目。方法簡單明了,以供參考。 ...
焦半徑公式橢圓 設M(m ,n)是橢圓x^2/a^2+ y^2/b^2=1(a>b>0)的一點,r1和r2分別是點M與點F₁(-c,0),F₂(c,0)的距離,那么(左焦半徑)r...
橢圓弦長公式是一個數學公式,關於直線與圓錐曲線相交求弦長,通用方法是將直線y=kx+b代入曲線方程,化為關於x(或關於y)的一元二次方程,設出交點坐標,利用韋達定理...
弦長公式d=√(1+k2)|x1-x2|=√[(1+k2)(x1-x2)2]=√(1+1/k2)|y1-y2|=√[(1+1/k2)(y1-y2)2]推導如下:由直線的斜率公式:k=(y1-y2)/(...
②如圖1,若設∠AFD= ,並分別過A、F作FD和BH的垂線,則可證: 從而得焦點弦長公式:|AB|= = 就是焦準距 。在雙曲線與拋物線中也有這樣的公式,如:在雙曲線...
中點弦拋物線中點弦公式 拋物線C:x^2(這裡x^2表示x的平方,下同)=2py上,過給定點P=(α,β)的中點弦所在直線方程為:py-αx=pβ-α^2。...
弦長的計算公式如下:弦切角的計算公式如下:注意: 亦即弦切角近似的等於切線角的三分之一。緩和曲線要素 迴旋線的曲線要素計算公式如下:...
詞條目錄 百科名片 簡介 發展歷程 標準方程 標準方程 特點 四種方程 切線方程 相關參數 術語解釋 解析式求法 光學性質 擴展公式 二次函式圖象 相關結論...
圓心角計算公式 編輯 ①L(弧長)=(r/180)XπXn(n為圓心角度數,以下同);...④K=2Rsin(n/2) K=弦長;n=弦所對的圓心角,以度計。圓心角性質 編輯 ...
