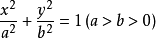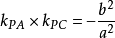共軛直徑

連結橢圓上任意兩點的線段叫弦，過橢圓中心的弦叫直徑。平行於直徑DE的弦的中點的軌跡 AB 和直徑 DE 互為共軛直徑。類似地可定義雙曲線的共軛直徑。

基本介紹

• 中文名：共軛直徑
• 橢圓：無數對
• 互相垂直：為橢圓的長軸和短軸
•  直徑：任意取

定義

一橢圓，其中心為 O ，過 O 任作一直徑 CD ，再作 CD 的平行弦 EF ，取 EF 的中點 M ，連線 OM 得橢圓的另一直徑 AB ，則 AB 、 CD 稱為橢圓的一對共軛直徑， EF 為直徑 AB 的共軛弦。因此，橢圓的任一條直徑必平分其共軛弦。由於上述 AB 直徑是任意取的，因此橢圓的共軛直徑有無數對。

當一對共軛直徑互相垂直時，即為橢圓的長軸和短軸。

圖1

橢圓共軛直徑

簡介

把經過橢圓 E ： 的中心的弦 AC 稱為橢圓的直徑，若 P 為橢圓 E 上異於 A 、C 的點 ， 則有 。若橢圓的兩直徑的斜率之積為 ，則稱這兩直徑為橢圓的共軛直徑。

特別地，若一直徑所在的斜率為0，另一條直徑的斜率不存在時，也稱這兩直徑為共軛直徑。

性質

性質一

設 AC，BD 為橢圓 E 的一對共軛直徑，若 A、B 兩點的坐標分別為 (x₁，y₁)、(x₂，y₂) ，則

（1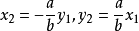） 或 ；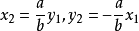

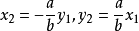
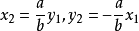
（2） ；

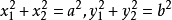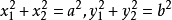
（3） ；

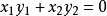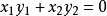
（4） ；

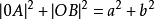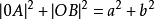
（5） 。

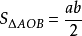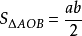
性質二

設 AC，BD 為橢圓 E 的一對共軛直徑， P 為橢圓 E 上任意一點，則 。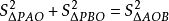

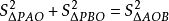
性質三

設 AC，BD 為橢圓 E 的一對共軛直徑， M 為線段 AB 的中點，射線 OM 交橢圓 E 於點 P ，則 。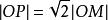

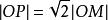
性質四

設 AC，BD 為橢圓 E 的一對共軛直徑，P 為橢圓 E 上任意一點，過 P 作 BD，AC 的平行線，分別交AC，BD 於 M，N ，則 。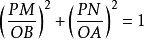

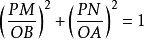
性質五

設 AC，BD 為橢圓 E 的一對共軛直徑，P 為橢圓 E 上任意一點，過 P 作橢圓 E 的切線分別交AC，BD 的延長線於 J、I，過M 分別作 BD 、AC 的平行線，分別交AC，BD 於 M、N，則