基本介紹
- 中文名:自配極四面形
- 外文名:self-polarity tetrahedron
- 所屬學科:數學
- 所屬問題:高等幾何(射影)幾何
- 別稱:自配極四面體
- 簡介:關於二階曲面∑的特殊四面體
基本概念,相關介紹,
基本概念
通過二次曲面外一點P的直線與曲面相交於X,Y兩點,如果關於X,Y,點P的調和共軛點為Q,則點Q的軌跡是平面。這個平面 稱為關於二次曲面的點P的極面(polarplane),點P稱為這個平面π的極點或極(pole)。當點P的極面通過點Q時,點Q的極面通過點P,這時稱P,Q兩點對於二次曲面是共軛的(conjugate)。當P點在二次曲面上時,可以認為極面是在P點的切平面。關於無奇點的二次曲面,當四面形各頂點的極面是對應於它的頂點的平面時,這個四面形稱為自配極四面形(selfpolar tetrahedron)。四面形A的四個頂點的關於二次曲面的極面為四面形B的平面時,交換A,B後也有同樣的性質。這樣的兩個四面形,稱為關於二次曲面互為配極四面形(polartetrahedron)。關於二次曲面,當兩個平面中一個平面的極點在另一個平面上時,稱這兩個平面關於二次曲面是共軛的(conjugate)。
稱為關於二次曲面的點P的極面(polarplane),點P稱為這個平面π的極點或極(pole)。當點P的極面通過點Q時,點Q的極面通過點P,這時稱P,Q兩點對於二次曲面是共軛的(conjugate)。當P點在二次曲面上時,可以認為極面是在P點的切平面。關於無奇點的二次曲面,當四面形各頂點的極面是對應於它的頂點的平面時,這個四面形稱為自配極四面形(selfpolar tetrahedron)。四面形A的四個頂點的關於二次曲面的極面為四面形B的平面時,交換A,B後也有同樣的性質。這樣的兩個四面形,稱為關於二次曲面互為配極四面形(polartetrahedron)。關於二次曲面,當兩個平面中一個平面的極點在另一個平面上時,稱這兩個平面關於二次曲面是共軛的(conjugate)。

當兩個平面束有射影關係時,其對應的二平面交線的軌跡一般是單葉雙曲面或雙曲拋物面。特別是當平面束的軸相交時,這個軌跡是二次錐面,軸互相平行時為二次柱面(即橢圓柱面或雙曲柱面),當考慮不在同一平面上的二直線的射影對應時,通過其對應點的直線的軌跡也成為二次曲面(M.Chasles)。
相關介紹
設r,s是任意一直徑p的共軛平面π與曲面的交線K的任意一對共軛直徑,則[p,r],[p,s]是曲面的一對共軛直徑平面。
因r,s是任意的,且屬於同一對合,故通過p有無限對共軛直徑平面,且也屬於同一對合;這個對合的固定元素是曲面通過P的二切面。
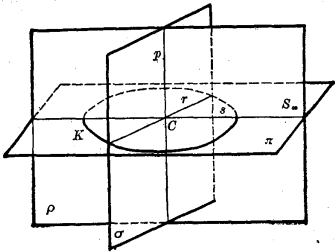 圖1
圖1設C是一二次曲面的中心,則一般可以引一個而且只有一個平面π通過C且共軛於p,π稱為p的一個共軛直徑平面,或稱p為π的一條共軛直線。所以,對於一個有心二次曲面的任一直徑p必存在一個共軛直徑平面與它對應,這個平面π的極點就是p的象 ,其次, 在π上取其與曲面相交的曲線K的任意兩條共軛直徑r,s,於是得到三個平面[r,s]≡π,[p,s]≡ρ,[p,r]=σ,其中任二平面是共軛平面,因而這三個平面構成一個自配極三面形,它與t=0構成一個自配極四面體、自配極三面形的三條棱稱為二次曲面的三條共軛直徑、由這個作圖法就可以知道,通過中心C存在無限組共軛平面p,σ,π。
,其次, 在π上取其與曲面相交的曲線K的任意兩條共軛直徑r,s,於是得到三個平面[r,s]≡π,[p,s]≡ρ,[p,r]=σ,其中任二平面是共軛平面,因而這三個平面構成一個自配極三面形,它與t=0構成一個自配極四面體、自配極三面形的三條棱稱為二次曲面的三條共軛直徑、由這個作圖法就可以知道,通過中心C存在無限組共軛平面p,σ,π。


