基本介紹
基本介紹
 笛卡爾
笛卡爾歷史介紹
出現原因
笛卡爾研究
 費馬是一個業餘從事數學研究的學者
費馬是一個業餘從事數學研究的學者 紀念笛卡兒發明解析幾何的郵票
紀念笛卡兒發明解析幾何的郵票費馬研究
基本內容
笛卡爾坐標系
 學習用品中的圓錐曲線
學習用品中的圓錐曲線新數學概念
學科套用
研究對象
 解析幾何
解析幾何坐標法
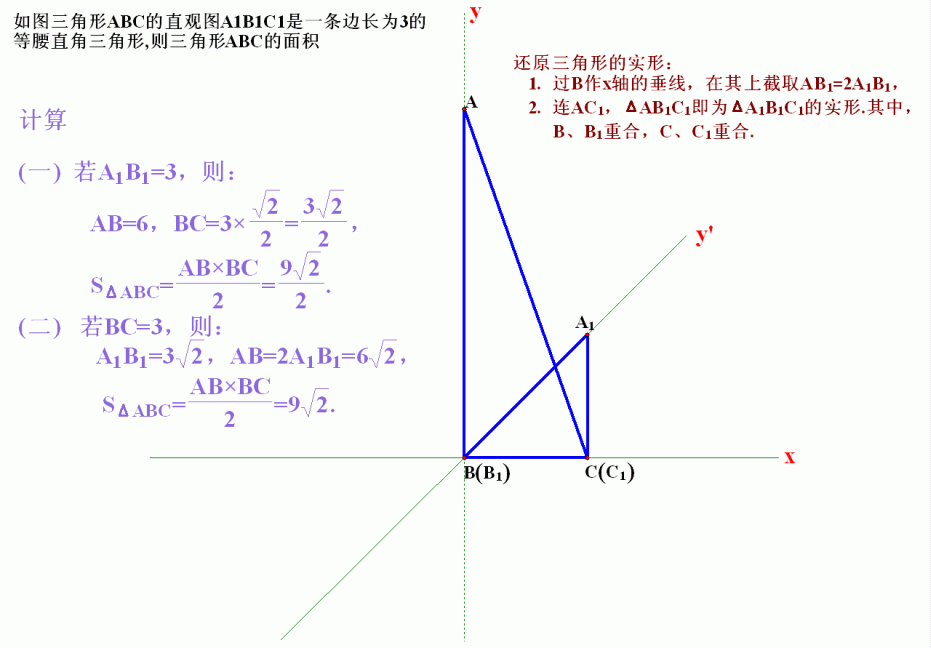 一道較難的解析幾何問題
一道較難的解析幾何問題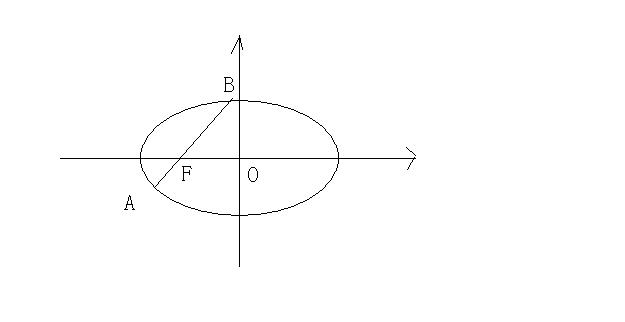
 笛卡爾
笛卡爾 費馬是一個業餘從事數學研究的學者
費馬是一個業餘從事數學研究的學者 紀念笛卡兒發明解析幾何的郵票
紀念笛卡兒發明解析幾何的郵票 學習用品中的圓錐曲線
學習用品中的圓錐曲線 解析幾何
解析幾何 一道較難的解析幾何問題
一道較難的解析幾何問題解析幾何指藉助笛卡爾坐標系,由笛卡爾、費馬等數學家創立並發展。它是利用解析式來研究幾何對象之間的關係和性質的一門幾何學分支,亦叫做坐標幾何。嚴格地講,解析...
解析幾何(Analytic geometry),又稱為坐標幾何(Coordinate geometry)或卡氏幾何(Cartesian geometry),早先被叫作笛卡兒幾何,是一種藉助於解析式進行圖形研究的幾何學...
平面解析幾何,又稱解析幾何(英語:Analytic geometry)、坐標幾何(英語:Coordinate geometry)或卡氏幾何(英語:Cartesian geometry),早先被叫作笛卡兒幾何,是一種藉助於...
《空間解析幾何》是2004年7月武漢大學出版社出版的圖書,作者是楊文茂。該書主要講述了幾何的概念及如何將幾何套用到自然科學領域等有關的內容。...
《解析幾何(第2版)》是北京大學數學系解析幾何課程的教材。主要講述解析幾何的基本內容和基本方法,包括:向量代數、空間直線和平面、常見曲面、坐標變換、二次曲線...
《解析幾何》是2010年華東理工大學出版社出版的圖書,作者是秦衍。...... 《解析幾何》 [1] 共分六章,主要論述了向量代數、空間的平面和直線、常見曲面、二次曲...
《解析幾何學》是2008年8月浙江大學出版社出版的圖書,作者是沈一兵、盛為民、張希、夏巧玲。...
解析幾何法是通過建立坐標系,把幾何的基本元素點和代數的基本研究對象數對應起來,利用代數工具解決幾何問題的方法。它的起源可以追溯到古希臘數學家對圓錐曲線的研究,...
《高等代數與解析幾何》一書是由曾令淮、段輝明、李玲幾人共同編寫而成,全書涵蓋現行理工科所用的高等代數教材內容以及空間解析幾何的基礎知識,內容包含三部分:空間...
《解析幾何(第三版)》是2015-08-07出版的圖書,作者是丘維聲。...... 《解析幾何(第三版)》是2015-08-07出版的圖書,作者是丘維聲。[1] 書名 解析幾何(第三...
《高等學校教材:空間解析幾何》根據綜合大學、師範院校數學類專業的空間解析幾何課程大綱編寫,共分五章,研究了矢量與坐標,平面與空間直線,空間曲面與空間曲線,柱面、...
《解析幾何的技巧》是2009年出版的圖書,作者是單墫。...... 《解析幾何的技巧》講述了:“幾何難!” 很多人有這樣的感慨。感謝笛卡爾發明了解析幾何,為解決幾何問...
《空間解析幾何》是2004年出版的圖書,作者是黃宣國。...... 《空間解析幾何》是2004年出版的圖書,作者是黃宣國。目錄 1 書籍信息 2 內容簡介 3 圖書目錄 ...
《解析幾何教程》是2012年江蘇大學出版社出版的圖書,作者是蔡國梁。主要講述了直角坐標系、向量代數、空問平面與直線等。...
《全國卷高考數學滿分教程:解析幾何》是2017年清華大學出版社出版的圖書,作者是周韡、李紅慶。...
《幾何講義第一學期解析幾何》是1992年高等教育出版社出版的圖書,作者是M.M.Postnikov。...
線性代數與解析幾何是大學數學教程系列教材的第二冊(線性代數與空間解析幾何),內容包括矩陣與行列式、向量與向量空間、線性方程組、特徵值與矩陣對角化、二次型與二...
《高中數學-解析幾何》是2008年7月龍門書局出版的圖書,作者是佟志軍。...... 《龍門專題:高中數學(解析幾何)(新課標)》是《龍門專題》系列中的一本,1.《龍門專...
全國卷滿分秘籍·解析幾何篇 作者:張永輝、王安平、張傑、張宏衛、余臣 定價:35元 印次:1-1 ISBN:9787302494096 出版日期:2018.01.01 印刷日期:2018.02.07 本...
本書主要講述解析幾何的基本內容和基本方法,包括:向量代數、空間直線和平面、常見曲面、坐標變換、二次曲線方程的化簡、正交變換、仿射變換、射影平面和射影變換等。...
《空間解析幾何第二版》是1997年01月武漢大學出版社出版的圖書。...... 《空間解析幾何第二版》是1997年01月武漢大學出版社出版的圖書。書名 空間解析幾何第二版...
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。...
解析法又稱為分析法,它是套用解析式去求解數學模型的方法。...... 運用坐標法解決問題的步驟是:首先在平面上建立坐標系,把已知點的軌跡的幾何條件“翻譯”成解析...
本書共分為三編,分別為:第一編平面上的直線;第二編橢圓、雙曲線、拋物線;第三編二階曲線的一般理論.本書適合大學生、中學生及平面解析幾何愛好者閱讀...
《高等代數與解析幾何(下)》是2007年清華大學出版社出版的圖書,作者是易忠。本書較系統地介紹了高等代數與解析幾何的基本理論、方法和某些套用。...
本書除涵蓋了數學各專業必備的空間解析幾何知識外,還包含大量的幾何套用方面的信息,特別是工程上的套用實例。 本書可作為數學各專業的空間解析幾何課的教材,同時亦...
