基本介紹
基本介紹


 圖1.倍立方問題
圖1.倍立方問題背景介紹
相關傳說
尺規作圖法
- 直尺:一側為無窮長的直線,沒有刻度也無法標識刻度的工具。只可以讓筆摹下這個直線的全部或一部分。
- 圓規:由兩端點構成的工具。可以在保持兩個端點之間的距離不變的情況下,將兩個端點同時移動,或者只固定其中一個端點,讓另一個端點移動,作出圓弧或圓。兩個端點之間的距離只能取已經作出的兩點之間的距離,或者任意一個未知的距離。
問題敘述

倍平方問題



方法













 圖2.用有刻度的直尺來進行倍立方
圖2.用有刻度的直尺來進行倍立方證明

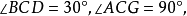




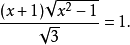




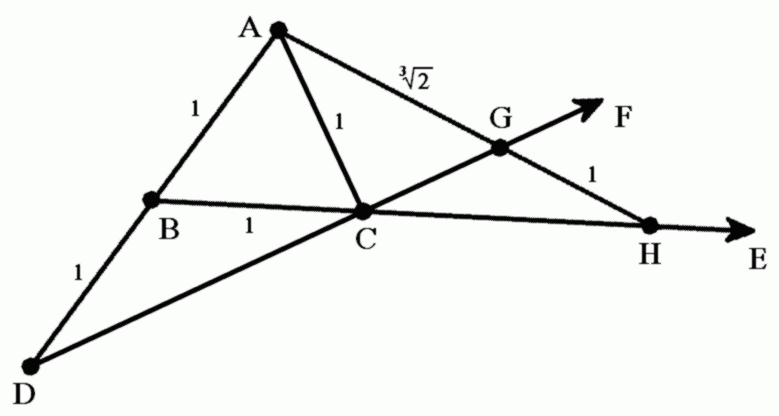


 圖1.倍立方問題
圖1.倍立方問題
















 圖2.用有刻度的直尺來進行倍立方
圖2.用有刻度的直尺來進行倍立方
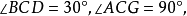








倍立方問題和三等分角問題、化圓為方問題共稱為尺規作圖不能問題,也叫做古希臘三大幾何問題。它指的是:作一個立方體,使它的體積是已知立方體的體積的兩倍。...
倍立方體問題(problem of duplication of a cube )是二千四百年前古希臘人提出的幾何三大作圖問題之一 。假設已知立方體的棱長是1個單位,那么這個立方體的體積便...
立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等,是幾何三大問題之一。假設已知立方體的棱長...
古希臘幾何作圖的三大問題是:①化圓為方,求作一正方形,使其面積等於一已知圓;②三等分任意角;③倍立方,求作一立方體,使其體積是一已知立方體的兩倍。這些問題...
立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等,是幾何三大問題之一。假設已知立方體的棱長...
尺規作圖不能問題就是不可能用尺規作圖完成的作圖問題。這其中最著名的是被稱為幾何三大問題的古典難題:三等分角問題:三等分一個任意角;倍立方問題:作一個立方體...
(2)三等分角問題:即求一角使其角度是一已知角度的三分之一(可用只有一點刻度的直尺與圓規作出);(3)倍立方問題:即求一立方體的棱長,使其體積是一已知立方體...
三等分角是古希臘三大幾何問題之一。三等分角是古希臘幾何尺規作圖當中的名題,和化圓為方、倍立方問題被並列為古代數學的三大難題之一,而如今數學上已證實了...
圓錐曲線:希臘著名學者梅內克繆斯(公元前4世紀)企圖解決當時的著名難題“倍立方問題”(即用直尺和圓規把立方體體積擴大一倍)。他把直角三角形ABC的直角A的平分線...
尼科米迪斯(Nicomedes,約公元前250年前後)希臘數學家,他曾批評埃拉托塞尼(Eratosthenes)解決倍立方問題的方法,約公元前3世紀中期.他的主要數學著作是《論蚌線》。...
三等分角是古希臘三大幾何問題之一。三等分角是古希臘幾何尺規作圖當中的名題,和化圓為方、倍立方問題被並列為古代數學的三大難題之一,而如今數學上已證實了...
其實三等分角的問題是由求作正多邊形這一類問題所引起來的。第三個問題是倍立方。埃拉托塞尼(公元前276年~公元前195年)曾經記述一個神話提到說有一個先知者得到...
《地理學》、《地球的測量》、《倍立方問題》、《柏拉圖》、《論平均值》等埃拉托塞尼地球周長 編輯 原理是:選擇兩個在同一條子午線上的點(至少經度大致相同),...
門奈赫莫斯,是一名希臘數學家,主要業績是發現了圓錐曲線和用圓錐曲線解倍立方問題。...
超越數的證明,給數學帶來了大的變革,解決了幾千年來數學上的難題——尺規作圖三大問題,即倍立方問題、三等分任意角問題和化圓為方問題。隨著超越數的發現,這...
三等分角是古希臘平面幾何里尺規作圖領域中的著名問題,與化圓為方及倍立方問題並列為尺規作圖三大難題。尺規作圖是古希臘人的數學研究課題之一,是對具體的直尺和...
超越數的證明,給數學帶來了極大的變革,它證明了幾千年來數學上的難題——尺規作圖三大問題,即倍立方問題、三等分任意角問題和化圓為方問題都是尺規不能問題(...
也有廣大中學生和大學生喜聞樂見且妙趣橫生的數學問題、對弈遊戲和最新成果;還有...24日 倍立方問題136 25日 圓化方問題136 26日 水牛和乾草137 27日 四種病138...
這曲線的發現是為了解決倍立方問題。蔓葉線的英文名字「Cissoid」是曲線發現了100年後《Geminus》中出現的,意為「像常春藤的」。參考資料 1. Hazewinkel, Michiel...
此外,歐多克索斯還研究過“中末比”(後人稱黃金分割)和“倍立方”等著名的數學問題 [1] .根據歐德莫斯(Eudemus)在《幾何學史》中的記載,他在研究中末比時套用...
主要成就 現代群論的創始人之一 用群論系統化地闡述了五次及五次以上方程不能用公式求解 用群論解決了古代三大作圖問題中的兩個(三等分角和倍立方) 目錄...
