尺規作圖不能問題

尺規作圖不能問題就是不可能用尺規作圖完成的作圖問題。這其中最著名的是被稱為幾何三大問題的古典難題：三等分角問題：三等分一個任意角；倍立方問題：作一個立方體，使它的體積是已知立方體的體積的兩倍；化圓為方問題：作一個正方形，使它的面積等於已知圓的面積。在2400年前的古希臘已提出這些問題，直至1837年，法國數學家萬芝爾才首先證明“三等分角”和“倍立方”為尺規作圖不能問題。1882年德國數學家林德曼證明π是超越數後，“化圓為方”也被證明為尺規作圖不能問題。

另類作法

總述

人們用尺規解幾何三大作圖題屢遭失敗之後，一方面是從反面懷疑它是否可作；另一方面就很自然地考慮，假如跳出尺規作圖的框框，也就是不限用尺規，而是藉助於另外一些曲線，或者藉助於尺規以外的一些工具，是不是可解決這些問題呢？

人們發現，一旦跳出了尺規作圖的框框，問題的解決將是輕而易舉的.這方面的工作已經有許多人做過，而且取得了不少成就，下面的詞條內容就擇要介紹一二.

三等分任意角

★作法一尼科梅德斯(Nicomedes，公元前250年左右)方法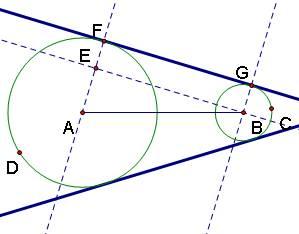

三等分角問題

對於已知銳角∠O，在角的一邊上取任意點B，作OB的垂線，交∠O的另一邊於點A.以O為定點，BA為定直線，2OA為定長，作出蚌線的右支C.從點A作BA的垂線，和蚌線C相交於點S，那么∠BOS=1/3∠BOA

★作法二

帕斯卡(Pascal，B.1623—1662)的方法

對於∠AOB，在其一邊上取任意長OA做半徑，以點O為圓心作一圓(圖12).延長AO，和圓O交於點C.以圓O為定圓，以C為定點，以定圓O的半徑為定長，作一蚶線和角的另一邊OB相交於點E.連結CE，過點O作OS∥CE，那么∠BOS=1/3∠BOA

★作法三

帕普斯(Pappus，約公元320年)方法

對於∠AOB，在它的兩邊上截取OA=OB.連結AB並三等分，設兩分點分別為C和D.以點C為中心，點A、D分別為頂點，作離心率e=√2的雙曲線.以點O為圓心，OB為半徑作弧，交雙曲線於點S.則∠BOS=1/3∠BOA

★作法四

玫瑰線方法

交∠AOB的兩邊於點A和B，分別以O和A為圓心，a為半徑畫弧，兩弧交於點S，則有∠BOS=1/3∠BOA

立方倍積

★作法一倍立方問題

倍立方問題

柏拉圖(Plato，公元前427—347年)的方法：作兩條互相垂直的直線，兩直線交於點O，在一條直線上截取OA=a，在另一條直線上截取OB=2a，這裡a為已知立方體的棱長.在這兩條直線上分別取點C、D，使∠ACD=∠BDC=90°(這隻要移動兩根直角尺，使一個角尺的邊緣通過點A，另一個角尺的邊緣通過點B，並使兩直角尺的另一邊重合，直角頂點分別在兩直線上，這時兩直角尺的直角頂點即為點C、D).線段OC之長即為所求立方體的一邊。

★作法二

門納馬斯(Menaechmus，約公元前375—325年)方法：從a∶x=x∶y=y∶2a可得

y2=2ax，x2=ay.所以，在直角坐標平面上畫出上述兩個二次方程所對應的兩條拋物線(圖16).這兩條拋物線交於O、A兩點，那么點A在x軸上的投影到原點的距離，就是所求的立方體的棱長。

★作法三

阿波羅尼(Apollonius de Perge，約公元前260—200年)方法：作一矩形ABCD，這裡AB=a、AD=2a.以此矩形對角線交點G為圓心，以適當長度為半徑作圓，與AB、AD之延長線分別交於E、F，使E、C、F三點共線，則AB∶DF=DF∶BE=BE∶AD，線段DF之長即為所求立方體的棱長。

化圓為方問題

★作法：對於已知圓O，化圓為方問題

化圓為方問題

作出它在第一象限的圓積線①l.連結這一圓積線的兩個端點B、F，過點B引BF的垂線BG，交x軸於G.在OA上取一點H，使HA=1/2GO.以H為圓心，HG為半徑畫弧，交y軸於點K.則以OK為一邊的正方形，即為所求作的與圓O等積的正方形。

積極意義

我們可以看出，幾何三大問題如果不限制作圖工具，便很容易解決.從歷史上看，好些數學結果是為解決三大問題而得出的副產品，特別是開創了對圓錐曲線的研究，發現了一批著名的曲線，等等.不僅如此，三大問題還和近代的方程論、群論等數學分支發生了關係.

相關趣事

阿納克薩戈勒斯是古希臘著名學者,在天文學中,他曾因解釋日,月食的成因而聞名遐邇,並且認識到月球自身並不發光.正是他出色的研究成果給他帶來了不幸,在他大約50歲的時候,橫禍從天而降,蒙受了冤獄之苦.災難的起因是他認為太陽是一塊熾熱的石頭.由於當時的宗教早已一口咬定太陽是神靈,而這位學者卻無視宗教的權威,說太陽是一塊石頭,因而被投入監獄。

儘管被囚禁的時間並不太長,可是,在被囚禁的日子裡冤屈,苦悶,無聊實在讓人度日如年.在陰暗,潮濕的牢房裡,阿納克薩戈勒斯看不到外面的朝霞暮靄,每天只有不長時間,陽光能穿過牢房那狹小的方形窗戶進入室內.每當陽光進入囚室,在牆壁上撒下一片光亮時,總會引起作為學者的他的種種聯想。

有一天,他在凝視圓圓的太陽賞賜給他的方形的光亮時,他那習慣于思索的頭腦突發奇想:能不能(僅用直尺和圓規)作一個正方形,使其面積與一個已知圓的面積恰好相等呢 就這樣,一道世界名題——"化圓為方"問題誕生了,它與"立方倍積"問題,"三等分任意角"問題一起被後人稱作古希臘幾何作圖三大難題. 阿納克薩戈勒斯想到化圓為方問題之後非常興奮,因為他身邊沒有書籍,沒有筆,很難研究別的問題,而這個問題卻不同,只要用草棍在地上畫就行了，草棍在牢房裡有的是。

他在進入高牆之前做夢也沒有想到,在他最痛苦的時候,是數學排除了他的幾分煩惱。

不過，他一生也未能解決他提出的這個問題。