化圓為方問題(problem of quadrature of circle)是二千四百多年前古希臘人提出的三大幾何作圖問題之一,即求作一個正方形,使其面積等於已知圓的面積。
基本介紹
- 中文名:化圓為方問題
- 外文名:problem of quadrature of circle
- 提出人:古希臘人
- 地位:三大幾何作圖問題之一
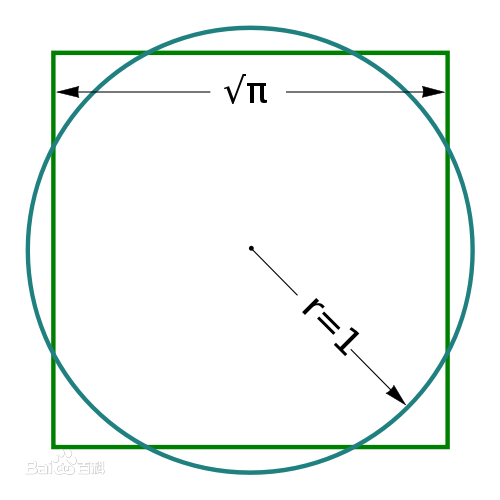
化圓為方問題(problem of quadrature of circle)是二千四百多年前古希臘人提出的三大幾何作圖問題之一,即求作一個正方形,使其面積等於已知圓的面積。
化圓為方問題(problem of quadrature of circle)是二千四百多年前古希臘人提出的三大幾何作圖問題之一,即求作一個正方形,使其面積等於已知圓的面積。...
化圓為方是古希臘尺規作圖問題之一,即:求一正方形,其面積等於一給定圓的面積。由π為超越數可知,該問題僅用直尺和圓規是無法完成的。但若放寬限制,這一問題...
倍立方問題和三等分角問題、化圓為方問題共稱為尺規作圖不能問題,也叫做古希臘三大幾何問題。它指的是:作一個立方體,使它的體積是已知立方體的體積的兩倍。...
古希臘幾何作圖的三大問題是:①化圓為方,求作一正方形,使其面積等於一已知圓;②三等分任意角;③倍立方,求作一立方體,使其體積是一已知立方體的兩倍。這些問題...
化圓為方問題(problem of quadrature of circle),也稱圓積問題,由古希臘著名學者阿納克薩戈勒斯提出的,但是阿納克薩戈勒斯一生也未能解決自己提出的問題。該問題為...
不可能用尺規作圖完成的作圖問題,稱為尺規作圖不能問題,如三等分角問題、化圓為方問題等。中文名 尺規作圖問題 外文名 problem of construction withruler and...
化圓成方是阿納克薩戈勒斯提出的數學問題,結果證明不可實現。...... 化圓成方是阿納克薩戈勒斯提出的數學問題,結果證明不可實現。中文名 化圓成方 性質 數學...
這其中最著名的是被稱為幾何三大問題的古典難題:三等分角問題:三等分一個任意角;倍立方問題:作一個立方體,使它的體積是已知立方體的體積的兩倍;化圓為方問題:作...
解的尺規作圖問題。根據尺規作圖準則,該方程之解無法作出,因此,立方倍積問題和三等分角問題、化圓為方問題一起,成為古希臘三大幾何難題。立方倍積問題不能用尺規...
它跟化圓為方問題是不同的:使用尺規作圖的方法令圓形的面積變成正方形的面積,這是不可能的。塔斯基的問題使用了(不可證的)選擇公理來分割圓令成為一塊塊數目...
《著名幾何問題及其解法》是2008年高等教育出版社出版的圖書,作者是(美)B....第Ⅵ章 化圓為方問題第Ⅶ章 正多邊形的作圖問題第Ⅷ章 最後的評述...
這一問題與三等分角問題、化圓為方問題,構成了初等幾何作圖中的三大作圖不能問題。2倍立方體問題之所以不能解決,是因為作圖時只能使用圓規和無刻度的直尺。這是古...
割圓曲線(quadratrix)亦稱圓積線,一類特殊曲線,指解決化圓為方問題的曲線。求作一個正方形,使它的面積與已知圓的面積相等,稱為化圓為方問題。凡是可以用來解決...
證明某些數是超越數有著重大的意義,比如說π的超越性的證明就徹底地解決了古希臘三大作圖問題中的化圓為方問題,即化圓為方是不可能的。判斷某些給定的數是否超越...
從此,這個問題在一些人中間傳來傳去,當時,三等分角和化圓為方問題已在社會上“臭名昭著”,而“四色瘟疫”又悄悄地傳播開來了。...
他用此定理去研究化圓為方問題,由於他的疏忽,而用了不正確的推論,以致有一時期有人誤認為化圓為方的問題已經解決,實際上化圓為方是一個尺規作圖不能問題 [1...
最著名的是被稱為幾何三大問題的三個古希臘古典作圖難題:立方倍積問題、三等分任意角問題和化圓為方問題.當時很多有名的希臘數學家,都曾著力於研究這三大問題,...
稍遲於阿基米德的阿波羅尼斯用圓柱螺線解決了化圓為方問題,如圖4-2-27所示。設圓O是一直圓柱之底面,A是螺旋線之起始點。螺旋線在其上任一點P處的切線交底所在...
早在公元前5世紀,古希臘學者安蒂豐為了研究化圓為方問題就設計一種方法:先作一個圓內接正四邊形,以此為基礎作一個圓內接正八邊形,再逐次加倍其邊數,得到正16...
“割圓曲線”等.“割圓曲線”是由該學派成員希皮亞斯(Hippias , (E ))創設的,目的是用它來三等分任意角,另一主要學者安蒂豐(Antiphon)在研究化圓為方問題時...
)……就是一個比用代數方法或許能求出化圓為方問題更困難得多的問題” 。李嘉圖的錯誤就在於試圖把“方”直接變成“圓”,在闡述方法上缺少歷史的和邏輯的“...
最著名的是被稱為幾何三大問題的三個古希臘古典作圖難題:立方倍積問題、三等分任意角問題和化圓為方問題.當時很多有名的希臘數學家,都曾著力於研究這三大問題,...
