基本介紹
- 中文名:超越數
- 外文名:transcendental number
- 提出時間:1844年
- 套用學科:數學
- 定義:不是代數的數
- 重要人物:劉維爾、厄米特、林德曼
定義
難題

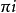
證明
常見形式

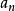



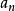
超越數的存在是由法國數學家劉維爾(Joseph Liouville,1809—1882)在1844年最早證明的。關於超越數的存在,劉維爾寫出了下面這樣一個無限小數:a=0.1...
《超越數》是一本哈爾濱工業大學出版社出版圖書。...... 超越數基本信息 編輯 作者:西格爾 出版社:哈爾濱工業大學出版社 譯者:魏道政 出版年:2011-3 頁數:61 定...
《數論Ⅳ:超越數》是2009年科學出版社出版的一本圖書,作者是A.N.Parshin / Shafarevich。...
全體複數分類兩類:代數數、超越數。超越數論研究數的超越性,其中對於歐拉常數與特定的黎曼ζ函式值之研究尤其令人感到興趣。...
超越方程(英語:transcendental equation)是包含超越函式的方程,也就是方程中有無法用自變數的多項式或開方表示的函式,與超越方程相對的是代數方程。超越方程的求解無法...
《超越數論基礎》是2011年哈爾濱工業大學出版社出版的圖書,作者是於秀源。本書主要介紹了超越數的基本理論和重要的研究方法。...
超越式是非代數式的解析式,指不能對變數字母和數用有限次加、減、乘、除、乘方、開方運算表示的解析式。它包括無理數指數式、對數式、三角函式式、反三角函式...
本書較全面地講述了超越數論的基本結果和主要方法...... 超越數引論內容介紹 編輯 包括milbert第七問題的解,指數函式、對數函式、橢圓函式、E函式、Mahler型函式等...
超越函式(Transcendental Functions),指的是變數之間的關係不能用有限次加、減、乘、除、乘方、開方運算表示的函式。歐拉把約翰·貝努利給出的函式定義稱為解析函式,...
代數數是代數與數論中的重要概念,指任何整係數多項式的復根。所有代數數的集合構成一個域,稱為代數數域。不是代數數的實數稱為超越數,例如圓周率。...
《數論4:超越數》由科學出版社出版,作者為(俄羅斯)帕爾申 (Parshin.A.N.) (俄羅斯)I.R.Shafarevich。...
林德曼(Lindemann,1852~1939) ,德國人,他是十九世紀未與二十世紀初的數學家,其主要貢獻在於率先證明了圓周率Π是一個超越數,所謂超越數就是不能作為有理係數...
π是個無理數,即不可表達成兩個整數之比,是由瑞士科學家約翰·海因里希·蘭伯特於1761年證明的。 1882年,林德曼(Ferdinand von Lindemann)更證明了π是超越數,即...
林德曼-魏爾斯特拉斯定理(Lindemann–Weierstrass theorem)是一個可以用於證明實數的超越性的定理。它表明,如果 α1,...,αn 是代數數,在有理數 ℚ...
