基本介紹
預備知識
等勢
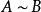
有限集與無限集
基數
定義
典例
實數集R
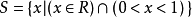
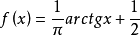
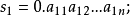
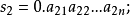
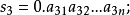
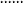
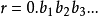
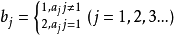
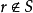
無理數集
區間 [0,1]
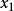

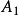
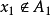

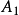
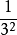
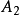
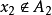
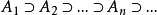
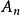
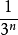
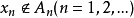
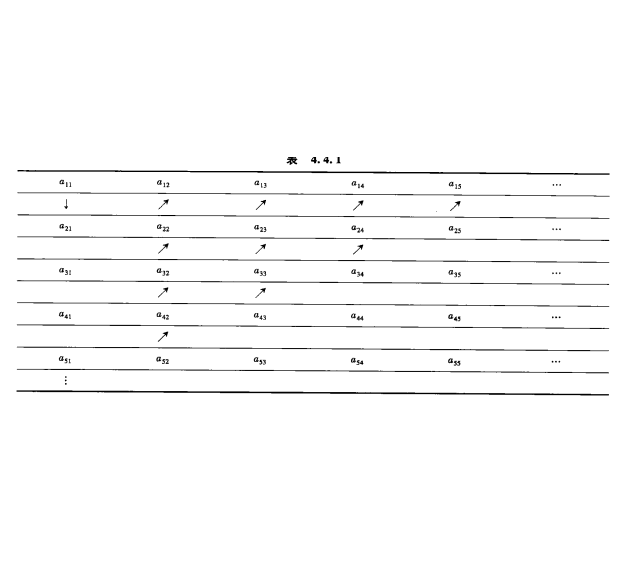
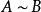
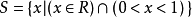
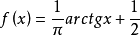
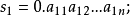
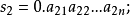
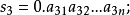
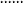
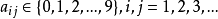
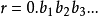
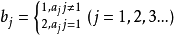
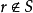
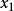

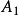
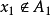

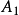
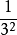
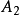
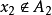
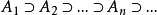
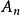
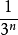
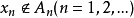
時,無法數出它們的元素個數,此時可通過“映射”的概念建立集合間的等勢關係,並拓廣集合中元素個數的概念,引進集合基數的概念,最後將集合分為可數集和不可數集。...
可數集(Countable set),是每個元素能與自然數集N的每個元素之間能建立一一對應的集合。如果將可數集的每個元素標上與它對應的那個自然數記號,那么可數集的元素就...
不可數基數(uncountable cardinal number)一種無窮基數...... 不可數基數(uncountable cardinal number)一種無窮基數.不可數集的基數統稱為不可數基數.一個無窮集合,如...
在數學中,首個不可數序數,傳統記之為ω1(或有時為Ω),是一個最小的序數,而其於被考慮為集合時為不可數。它是所有可數序數的最小上界。ω1 的所有元素,皆...
無限集合(infinite set)亦稱無窮集合,是一類特殊的集合,它有下面幾種定義:1.不是有限集的集合;2.可與其真子集對等的非空集合;3.既不是空集,又不與Mn={1,...
至多可數集是一類特殊的集合,有限集與可數集的統稱。有時稱有限集為有限可數集,可數集為無限可數集,至多可數集的子集是至多可數的,至多可數個至多可數集的...
比可數集合“大”的稱之為不可數集合,如實數集,其基數與自然數的冪集相同。由於一個無窮集合的冪集總是具有比它本身更高的基數,所以通過構造一系列的冪集,可以...
不可列集即“不可數集”。 ...... 不可列集即“不可數集”。 [1] 參考資料 1. 金炳華等編.哲學大辭典(修訂本) (上、下冊):上海辭書出版社,2001年06月...
可數集在數學上,可數集,或稱可列集、可數無窮集合,是與自然數集的某個子集具有相同基數(等勢)的集合。在這個意義下不是可數集的集合稱為不可數集。這個術語是...
1.7 可數集.不可數集,基數1.8 選擇公理和Tukey引理1.9 集族的笛卡兒積第二章 拓撲空間與連續映射2.1 度量空間與連續映射2.2 拓撲空間與連續映射...
不可數集合examples: 1)“所有整數數列(無窮個整數的排列)的集合”是不可數的;[對角論證法,康托爾] 2)“所有實數的集合”…. 3)“所有函式的集合”…....
其標記符號為 ℵ (由希伯來字母 א 演變而來)加角標表示可數集(包括自然數)的勢標記為ℵ₀ ,下一個較大的勢為ℵ₁ ,再...
康托爾集P具有三條性質:1、P是完備集。2、P沒有內點。3、P的基數為c。4、P是不可數集。康托爾集是一個基數為c的疏朗完備集。...
Georg Ferdinand Ludwig Philipp,1845.3.3-1918.1.6)德國數學家,集合論的創始...同年又構造了實變函式論中著名的“康托爾集”,給出測度為零的不可數集的一...
與 均為不可數集,且基數均為連續統基數。對於 的方塊 ,存在一個一一映射同理存在一個一一映射由於 與 基數相同,故存在一個一一映射但該映射不一定是連續的。...
尤其集合論(其語言可數)有可數的模型,這個被稱為Skolem佯謬,雖然它是真的(如果你接受集合論公理的話)。如果要知道為什麼它被認為是佯謬,讓我們考慮集合論中假設不...
