基本介紹
- 中文名:至多可數集
- 所屬學科:數學(集合論)
- 簡介:有限集與可數集的統稱
基本介紹



相關定理


例題解析


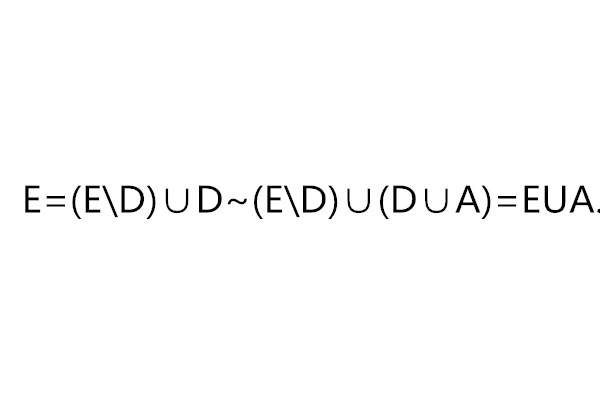







至多可數集是一類特殊的集合,有限集與可數集的統稱。有時稱有限集為有限可數集,可數集為無限可數集,至多可數集的子集是至多可數的,至多可數個至多可數集的...
可數集(Countable set),是指每個元素都能與自然數集N的每個元素之間能建立一一對應的集合。如果將可數集的每個元素標上與它對應的那個自然數記號,那么可數集的元素...
如果集合是有限集合或者是可數集,那么稱為至多可數的。 ...... 如果集合是有限集合或者是可數集,那么稱為至多可數的。V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
可數選擇公理,指示為ACω,是公理化集合論的類似於選擇公理的一個公理。它聲稱非空集合的任何可數蒐集都一定有選擇函式。保羅·寇恩證明了ACω在Zermelo-Fraenkel...
從勒貝格可測集合的定義中,可以證明所有這類的集合都滿足以下兩個性質:(1)測度是可數可加的,也就是說,如果Ai是最多可數個兩兩不交的集合,那么 。...
如果R中的點集A可以表成至多可數個疏朗集的並,就稱A是第一範疇集(或第一綱集)。...... 如果R中的點集A可以表成至多可數個疏朗集的並,就稱A是第一範疇...
Y為平庸拓撲空間,或者X為至多可數集並且Y為 空間。定理2 設X為任一集合,Y為一個拓撲空間,則映射空間 (點式收斂拓撲)為 ( 正則,完全正則,連通,路連通,緊緻...
誠然,問題涉及數理邏輯和集合論,但它一開始就牽涉到無窮集合,而現代數學如果脫離無窮集合就可以說寸步難行。因為如果只考慮有限集合或至多是可數的集合,那絕大部分...
因為如果只考慮有限集合或至多是可數的集合,那絕大部分數學將不復存在。而且即便這些有限數學的內容,也有許多問題要涉及無窮的方法,比如解決數論中的許多問題都要用...
在數理邏輯中,經典勒文海姆–斯科倫定理對於標識的任何可數一階邏輯語言 L 和 L-結構 M,存在一個可數無限基本子結構 。這個定理的自然和有用的推論是所有一致的...
