基本介紹
- 中文名:無限集合
- 外文名:infinite set
- 別稱:無窮集合
- 屬性:一類特殊的集合
- 所屬學科:數學(集合論)
基本介紹













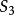
 圖1
圖1

無限集合研究的基本方法

 圖2計算有限集合技術的過程
圖2計算有限集合技術的過程可數無限集合




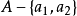





 圖3 集合ZXZ中元素排列方法
圖3 集合ZXZ中元素排列方法不可數無限集合
無窮集合基數的比較

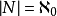




















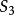




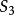
 圖1
圖1


 圖2計算有限集合技術的過程
圖2計算有限集合技術的過程



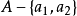





 圖3 集合ZXZ中元素排列方法
圖3 集合ZXZ中元素排列方法
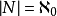










無限集合(infinite set)亦稱無窮集合,是一類特殊的集合,它有下面幾種定義:1.不是有限集的集合;2.可與其真子集對等的非空集合;3.既不是空集,又不與Mn={1,...
集合,簡稱集,是數學中一個基本概念,也是集合論的主要研究對象。集合論的基本理論創立於19世紀,關於集合的最簡單的說法就是在樸素集合論(最原始的集合論)中的定義...
數學集合在數學上是一個基礎概念。基礎概念是不能用其他概念加以定義的概念,也是不能被其他概念定義的概念。集合的概念,可通過直觀、公理的方法來下“定義”。集合...
集合的勢是用來度量集合規模大小的屬性的。對於有限集合,可用集合的元素個數來進行度量,對於無限集合這個辦法就行不通了,為此我們需要採用一種新的方法來比較兩個...
無限符號(∞),無窮或無限,即“沒有邊界”的意思。它在神學、哲學、數學和日常生活中有著不同的概念。通常使用這個詞的時候並不涉及它的更加技術層面的定義。...
D無限集(D-infinite set)一種無限集.若存在集合A到自己的真子集的雙射,則稱A為D無限集.任何一個集合不是D有限集就是D無限集.例如自然數集是D無限集.}A}...
無限群指元素個數為無限的群。拓撲群,李群,(無限)典型群,代數群,算術群,都是無限群。無限群的研究開始於19世紀下半葉。正當抽象群的概念形成之際,數學家們...
絕對無限(Absolute Infinite) 是數學家康托爾的超越超限數的無限概念。康托爾把絕對無限等同於神。他堅持絕對無限有各種數學性質,包括絕對無限的所有性質也被某些更...
《無限》是飛兒樂團於2005年4月8日發行的第二張專輯,共收錄13首歌曲。專輯的製作人是MikePela和陳建寧。2005年,該專輯獲得全球華語歌曲排行榜“最佳專輯獎”。...
實無限是在數學基礎研究中,把無限作為一種已經形成了的對象來加以考察。持此實無限觀點的最早的代表是柏拉圖。...
集合存在性公理(existence axiom of set)是GB系統的集合論公理,指GB系統中的第3組(即C組)公理,共有4條,包括無窮公理,並集公理,冪集公理,和替換公理。...
無限布爾代數是一種常用的布爾代數,指論域B是無限集的布爾代數。...... 無限布爾代數是一種常用的布爾代數,指論域B是無限集的布爾代數。無限集S的冪集代數<P(...
策略是局中人在對策中採用的一個可行的自始至終通盤籌劃的行動方案,局中人策略的全體稱為策略集合,它可以是有限集,也可以是無限集。...
曼德布洛特集合(Mandelbrot set)是在複平面上組成分形的點的集合,一種分形圖案。...... 曼德布洛特集合就是使以上序列不延伸至無限大的所有c點的集合。從數學上來講...
無限裝殖章節目錄 編輯 第一集 叢林逃亡第一章 死刑 第二章 入獄 第三章 亡命 第四章 眾神的遊戲 第五章 御神裝殖 第六章 女人 第七章 林瑤也來了 ...
《無限中洲隊》是小虛小乖創作的網路小說,發表於起點網。...... 他們的世界是無限的平行的集合,所以更不可能會被平行中的某個作者完全控制,擺弄於鼓掌之間,作者能...
嵌套無限,簡而言之,是一層又一層,無限層嵌套的無限,是用來描述物質系統層級的一種方式,而我們很有可能就生活在某個嵌套無限世界中的某個無限小微元粒子中的無限...
無窮或無限,來自於拉丁文的“infinitas”,即“沒有邊界”的意思。其數學符號為∞。它在科學、神學、哲學、數學和日常生活中有著不同的概念。通常使用這個詞的時候...
給定兩個集合A,B,把他們所有的元素合併在一起組成的集合,叫做集合A與集合B的並集,記作A∪B,讀作A並B。...
這個點集均出自公式:Zn+1=(Zn)^2+C,對於非線性疊代公式Zn+1=(Zn)^2+C,所有使得無限疊代後的結果能保持有限數值的複數C的集合,構成曼德勃羅集。 [1] ...
