並集

給定兩個集合A，B，把他們所有的元素合併在一起組成的集合，叫做集合A與集合B的並集，記作A∪B，讀作A並B。

基本介紹

• 中文名：並集
• 外文名：union
• 符號：∪
• 概念：把A與B合併在一起組成的集合
• 關鍵字：並集、交集
• 套用學科：數學

定義

若A和B是集合，則A和B並集是有所有A的元素和所有B的元素，而沒有其他元素的集合。A和B的並集通常寫作 "A∪B"，讀作“A並B”，用符號語言表示，即：A∪B={x|x∈A,或x∈B}

形式上，x是A∪B的元素，若且唯若x是A的元素，或x是B的元素。

代數性質

二元並集（兩個集合的並集）是一種結合運算，即A∪(B∪C) = (A∪B) ∪C。事實上，A∪B∪C也等於這兩個集合，因此圓括弧在僅進行並集運算的時候可以省略。相似的，並集運算滿足交換律，即集合的順序任意。

空集是並集運算的單位元。 即 ∅ ∪A=A。對任意集合A，可將空集當作零個集合的並集。

結合交集和補集運算，並集運算使任意冪集成為布爾代數。 例如，並集和交集相互滿足分配律，而且這三種運算滿足德·摩根律。 若將並集運算換成對稱差運算，可以獲得相應的布爾環。

無限並集

最普遍的概念是：任意集合的並集。若 M 是一個集合的集合，則 x 是 M 的並集的元素，若且唯若存在 M 的元素 A，x 是 A 的元素。即：

無論集合 M 本身為何，M 的並集是一個集合，這就是公理集合論中的並集公理。

例如：A ∪ B ∪ C 是集合 {A,B,C} 的並集。同時，若 M 是空集， M 的並集也是空集。有限並集的概念可以推廣到無限並集。

上述概念有多種表示方法：集合論科學家簡單地寫， 而大多數人會寫為。 後者可推廣為 ， 表示集合 {Ai : i is in I} 的並集。這裡是一個集合，是一個的集合。在索引集合是自然數集合的情況下，上述表示和求和相類似：

同樣，也可以寫作 "A1 ∪ A2 ∪ A3 ∪ ···". （這是一個可數的集合的並集的例子，在數學分析中非常普遍；參見σ-代數）。最後，要注意的是，當符號"∪" 放在其他符號之前，而不是之間的時候，要寫的大一些。 交集在無限並集中滿足分配律，即 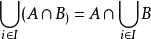，。 結合無限並集和無限交集的概念，可得

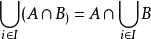
性質

韋恩圖表示

可用韋恩圖表示（分為五種情況顯示）

用韋恩圖解釋“並集”的概念

【說明】並集的意義：A∪B，即A∪B是所有A、B中的元素組成的集合，因此，A∪B中的元素至少具有集合A或集合B的屬性之一。

交集的性質

關於交集有如下性質：

A∩B A，A∩B B，A∩A=A，A∩ = ,A∩B=B∩A；

並集的性質

關於並集有如下性質：

A∪B，B A∪B，A∪A=A，A∪∅=A,A∪B=B∪A

若A∩B=A，則A∈B，反之也成立；

若A∪B=B，則A∈B，反之也成立。

若x∈（A∩B），則x∈A且x∈B；

若x∈（A∪B），則x∈A，或x∈B。

舉例

集合{1, 2, 3} 和 {2, 3, 4} 的並集是 {1, 2, 3, 4}。數字 9 不屬於質數集合 {2, 3, 5, 7, 11, …} 和偶數集合{2, 4, 6, 8, 10, …} 的並集，因為 9 既不是素數，也不是偶數。

更通常的，多個集合的並集可以這樣定義：例如，A, B 和 C 的並集含有所有 A 的元素，所有 B 的元素和所有 C 的元素，而沒有其他元素。

形式上，x是 A∪B ∪C 的元素，若且唯若x ∈A 或 x ∈B 或 x ∈C。