集合運算是數學科學中常用的詞語,是一種非常有效的構造形體的方法,可以直觀的減少運算難度。
基本介紹
- 中文名:集合運算
- 套用領域:數學科學
- 釋義:一種非常有效的構造形體的方法
- 適用:正則集與正則集合運算運算元
概念
主要類型
分類
集合的運算
- {1, 2}∪{紅色, 白色} = {1, 2, 紅色, 白色}
- {1, 2, 綠色}∪{紅色, 白色, 綠色} = {1, 2, 紅色, 白色, 綠色}
- {1, 2}∪{1, 2} = {1, 2}

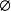

- A⊆B ⇒ A∩B = A

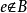


集合運算是數學科學中常用的詞語,是一種非常有效的構造形體的方法,可以直觀的減少運算難度。

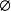


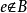

集合運算是數學科學中常用的詞語,是一種非常有效的構造形體的方法,可以直觀的減少運算難度。...
運算,數學上,運算是一種行為,通過已知量的可能的組合,獲得新的量。運算的本質是集合之間的映射。一般說來,運算都指代數運算,它是集合中的一種對應。對於集合A中...
交集合是指對於集合A和集合B,由即屬於A又屬於B的所有元素所組成的集合。...... 記成A∩B,其中,“∩”看成是集合的運算符號,它是從兩個集合得到交集合的運算...
集合,簡稱集,是數學中一個基本概念,也是集合論的主要研究對象。集合論的基本理論創立於19世紀,關於集合的最簡單的說法就是在樸素集合論(最原始的集合論)中的定義...
數學集合在數學上是一個基礎概念。基礎概念是不能用其他概念加以定義的概念,也是不能被其他概念定義的概念。集合的概念,可通過直觀、公理的方法來下“定義”。集合...
除運算是一種非傳統的集合運算,是廣義笛卡兒積的逆運算。設有兩個關係R和關係S,其元數分別為n和m(n>m>0),則R和S進行除法的結果記為P=R÷S,其中P是一...
交運算有兩種含義,它可以指集合的交運算,即兩個集合的交集,與之對應的是集合的並運算,即兩個集合的並集;也可以指格的交運算,與之相對應的是格的結運算。...
基本運算是指執行運算最基礎的算法。在關係代數運算中,有5種基本運算,它們是並(U)、差(—)、投影、選擇、笛卡爾積(X),其它運算即交、連線和除,均可通過5種...
集合符號,英文名A collection of symbols,是數學的分支集合的表達符號,主要套用於計算機領域。...
mod運算,即求余運算,是在整數運算中求一個整數 x 除以另一個整數y的餘數的運算,且不考慮運算的商。在電腦程式設計中都有MOD運算,其格式為: mod(nExp1,nEx...
運算律是通過對一些等式的觀察、比較和分析而抽象、概括出來的運算規律。既是重要的數學規律,也是數學運算固有的性質。包括加法交換律和結合律、乘法交換律和結合律...
集合代數發展並描述了集合的基本性質和規律,集合論運算,如並集、交集、補集,以及集合的關係,如等於、包含。這門學科系統研究如何來表達和進行上述的運算和關係的操作...
關係的基本運算有兩類:一類是傳統的集合運算(並、差、交等),另一類是專門的關係運算(選擇、投影、連線、除法、外連線等),有些查詢需要幾個基本運算的組合,要...
1)整體與元素的關係.集合數據例如矩陣,從矩陣加到元素加,實現對集合元素的處理. 相同運算符對不同數據產生的計算效果可不同(例如C++語言的重載,多態等)。...
補運算是有補格中求補元的過程,在集合論中相當於補集運算。...... 補運算是有補格中求補元的過程,在集合論中相當於補集運算。中文名 補運算 釋義 有補格中...
曼德布洛特集合(Mandelbrot set)是在複平面上組成分形的點的集合,一種分形圖案。...... 一個給定的複數c或者屬於曼德布洛特集合M,或者不是。曼德勃羅集合計算的方法 ...
集合論中,設A,B是兩個集合,由所有屬於集合A且屬於集合B的元素所組成的集合,叫做集合A與集合B的交集(intersection),記作A∩B。...
給定兩個集合A,B,把他們所有的元素合併在一起組成的集合,叫做集合A與集合B的並集,記作A∪B,讀作A並B。...
補集一般指絕對補集,即一般地,設S是一個集合,A是S的一個子集,由S中所有不屬於A的元素組成的集合,叫做子集A在S中的絕對補集。在集合論和數學的其他分支中,...
