基本介紹
導言,基本結構,代數結構,序結構,結構的定義,對偶性原理,包含的代數,
導言
集合代數是研究集合運算和集合關係的基本性質的學科。研究這些性質可以深入探究集合的本質,也有助於實際套用。
像普通算術的表達和計算一樣,集合的表達和計算可能相當複雜。通過系統研究將有助於熟練使用和理解這些表達方式並進行計算。
在算術研究方面,是通過初等代數來研究算術的運算和關係的。
基本結構
集合上通常自然定義的結構包括:
包含( ):
): 若且唯若
若且唯若 ;
;



真包含( ):
): 若且唯若
若且唯若 且
且 ;
;




交( ):
): 定義為
定義為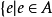 且
且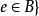 ;
;


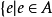
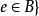
並( ):
): 定義為
定義為 或
或 ;
;




差( ):
): 定義為
定義為  且
且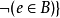 (亦稱相對補);
(亦稱相對補);



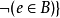
對稱差( ):
): 定義為
定義為  ;
;



補:補運算的前提是存在一個由上下文確定的全集X,其某個子集A對於X的補 定義為X-A。
定義為X-A。

其它運算
冪集: 定義為
定義為 。(A的冪集是A所有子集構成的集合)
。(A的冪集是A所有子集構成的集合)


特殊的集合
空集( ):沒有任何元素的集合。
):沒有任何元素的集合。

全集:這是一個由上下文確定的集合,通常上下文中其它的集合都是它的子集。
代數結構
代數結構是關於運算的結構。以下是集合間運算的基本性質:
- 冪等律
- 冪麼律
序結構
包含關係有如下性質:
自反性: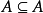 ;(任何集合都是其本身的子集)
;(任何集合都是其本身的子集)
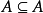
反對稱性: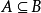 且
且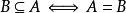 ;(這是證明兩集合相等的常用手段之一)
;(這是證明兩集合相等的常用手段之一)
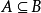
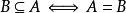
傳遞性: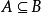 且
且 ;
;
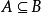

是集合間的一個非嚴格偏序關係。
真包含關係“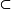 ”有如下性質:
”有如下性質:
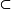
反自反性: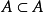 不成立;
不成立;
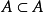
非對稱性: 不成立;反之亦然;
不成立;反之亦然;

傳遞性: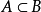 且
且 ;
;
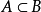

是集合間的一個嚴格偏序關係。
包含和真包含關係定義了集合間的一個偏序關係。在該偏序關係的意義下兩者等價,通常不失一般性地將該偏序關係指為  。
。

結構的定義
顯然,上面的所有結果並不是獨立的,大部分結果都可以從一個很小的結構推導出來。
比如很容易知道:
對稱差可以用並和差來定義。
補可以用差來定義。
真包含關係可以用包含關係來定義。
包含關係可以用並,交,差之一來定義,這是因為 等價於以下任一命題:
等價於以下任一命題:




命題 1:對全集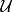 的任意子集A,下列恆等式成立:
的任意子集A,下列恆等式成立:
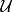
(1)同一性:

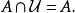
(2)補集律:

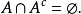
上述五組性質:交換律、結合律、分配律、同一性和補集律,可以說包含了集合代數的所有內容,可以認為集合代數中所有正確的命題都是從它們得到的。
對偶性原理
上述命題有一個有趣的形式,就是每一組恆等式都是成對出現的。將 ∪ 和 ∩,或者 Ø 和U相互交換,一個恆等式就變成了相應的另一個。
這是集合代數的一個非常重要的性質,稱作集合的對偶性原理。它對集合的所有真命題都有效。真命題通過相互交換 ∪ 和 ∩,Ø 和U,改變包含符號的方向得到的對偶命題也是真的。若一個命題和其對偶命題相同,則稱其為自對偶的。
包含的代數
下列命題說明包含是種偏序關係。
命題 2:若A,B,C 為集合,則下述成立:
(1)自反性:

(2)反對稱性:


(3)傳遞性:
若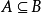 且
且 ,則
,則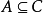 。
。
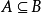

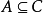
命題 3:若 A,B,C是集合 S 的子集,則下述成立:

(2)存在並運算:
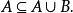
若 且
且 則
則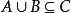 。
。


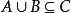
(3)存在交運算:
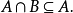
若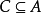 且
且 則
則 。
。
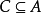


上述命題說明,集合的包含關係可以採用並集運算或交集運算來表示,即包含關係在公理體系中是多餘的。