最大元(greatest element)是偏序集中的一種特殊元素,指偏序集的子集中不小於一切的元素。與此相關的概念還有,極大元:指偏序集中沒有比它更大的可比較的元素;最小元:指偏序集的子集中小於或等於一切元素的元素;極小元:指偏序集中沒有與它可比較的更小的元素。
基本介紹
- 中文名:最大元
- 外文名:greatest element
- 涉及學科:離散數學
- 定義:偏序集的子集中不小於一切的元素
- 性質:偏序集中的一種特殊元素
- 相關:極小元、極大元、最小元
簡介,相關概念,偏序集,極小元,極大元,最小元,區別,
簡介
一種特殊元素,指偏序集的子集中不小於一切元素的元素。令<A,R>是偏序集, ,如果對每一個
,如果對每一個 都有xRb,則稱b是<B,R>的最大元。對給定的<B,R>不一定有最大元,若有最大元,則是惟一的。<A,R>的最大元稱為單位元,記為1。<B,R>的最大元是<B,R-1>的最小元;反之亦真。最大元是惟一的極大元。
都有xRb,則稱b是<B,R>的最大元。對給定的<B,R>不一定有最大元,若有最大元,則是惟一的。<A,R>的最大元稱為單位元,記為1。<B,R>的最大元是<B,R-1>的最小元;反之亦真。最大元是惟一的極大元。


相關概念
偏序集
定義1,設P是集合,P上的二元關係“≤”滿足以下三個條件,則稱“≤”是P上的偏序關係(或部分序關係):
(1)自反性:a≤a,∀a∈P;
(2)反對稱性:∀a,b∈P,若a≤b且b≤a,則a=b;
(3)傳遞性:∀a,b,c∈P,若a≤b且b≤c,則a≤c;
具有偏序關係的集合P為偏序集(或稱半序集),記為(P,≤)。a≤b讀作“a小於或等於b”或“a含於b”,a<b讀作“a小於b”或“a真含於b”。這裡a<b等價於a≤b且a≠b,∀a,b∈P。若a≤b或b≤a,則稱a與b是可比的,否則就說a與b是不可比。a與b不可比記作a||b。
定義2,設(P,≤)是偏序集,對於P中任意二元x,y有x≤y yRx,則稱R是≤的逆關係,記作≤-1。≤-1稱為≤的逆。
yRx,則稱R是≤的逆關係,記作≤-1。≤-1稱為≤的逆。

定理1,設(P,≤)是偏序集,則(P,≤-1)也是偏序集,偏序集(P,≤-1)稱為偏序集(P,≤)的對偶,簡記作P-1。
定義3,設(P,≤)是偏序集,N P,由於關係≤是P×P的子集,令≤N=≤∩(N×N)是≤與N×N的交集,則稱≤N是關係≤在N上的限制。
P,由於關係≤是P×P的子集,令≤N=≤∩(N×N)是≤與N×N的交集,則稱≤N是關係≤在N上的限制。

定理2,設(P,≤)是偏序集,關係≤N是≤在N上的限制,則(N,≤N)是偏序集,稱為(P,≤)的子偏序集。
極小元
偏序集中的一種特殊元素,指偏序集中沒有與它可比較的更小的元素。設<A,R>是偏序集, ,若不存在
,若不存在 ,使得 xRb 且 x≠b,則b稱為<B,R>的極小元。對給定的<B,R>可以有一個或多個極小元,也可以沒有極小元。若a與b是<B,R>的兩個不同的極小元,則
,使得 xRb 且 x≠b,則b稱為<B,R>的極小元。對給定的<B,R>可以有一個或多個極小元,也可以沒有極小元。若a與b是<B,R>的兩個不同的極小元,則 且
且 。當B為有限集時,<B,R>一定有極小元。
。當B為有限集時,<B,R>一定有極小元。




極大元
偏序集中的一種特殊元素,指偏序集中沒有比它更大的可比較的元素。設<A,R>是偏序集, ,若不存在
,若不存在 ,使得 bRx 且x≠b,則b稱為<B,R>的極大元。對給定的<B,R>可以有一個或多個極大元,也可以沒有極大元。若a與b是<B,R>的兩個不同的極大元,則
,使得 bRx 且x≠b,則b稱為<B,R>的極大元。對給定的<B,R>可以有一個或多個極大元,也可以沒有極大元。若a與b是<B,R>的兩個不同的極大元,則 且
且 。當B為有限集時,<B,R>一定有極大元。
。當B為有限集時,<B,R>一定有極大元。




最小元
一種特殊元素,指偏序集的子集中小於或等於一切元素的元素。令<A,R>是偏序集, ,如果對每一個
,如果對每一個 都有bRx,則稱b是<B,R>的最小元。對給定的<B,R>不一定有最小元,若有最小元,則是惟一的。<A,R>的最小元稱為零元素,記為0。<B,R>的最小元是<B,R-1>的最大元;反之亦真。最小元是惟一的極小元。
都有bRx,則稱b是<B,R>的最小元。對給定的<B,R>不一定有最小元,若有最小元,則是惟一的。<A,R>的最小元稱為零元素,記為0。<B,R>的最小元是<B,R-1>的最大元;反之亦真。最小元是惟一的極小元。


區別
設<A,R>偏序集,B含於A;
①若y∈B滿足任取x∈B,y≤x→x=y,則稱y為B的極大元;(箭頭表示“蘊含”)
②若y∈B滿足任取x∈B,x≤y,則稱y為B的最大元;
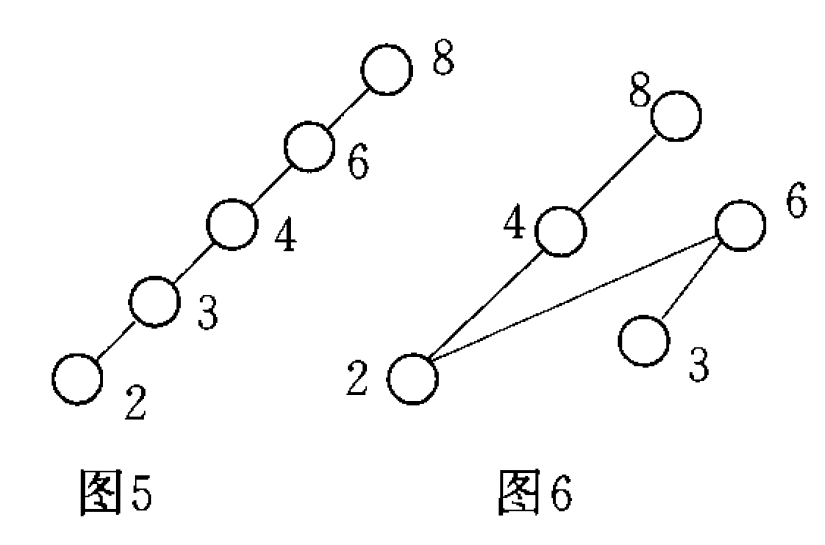
易得最大元必是極大元,但極大元不一定是最大元,應注意極大元和最大元的區別。 最大元是B中最大的元素,它與B中其它元素都可比;而極大元不一定與B中其它元素都可比,只要沒有比它大的元素,它就是極大元。對於有窮集合B,極大元一定存在,但最大元不一定存在。最大元如果存在一定是唯一的,但極大元可能有多個。
請注意極小元和最小元的區別。最小元是B中最小的元素,它與B中其它元素都可比;而極小元不一定與B中其它元素都可比,只要沒有比它小的元素,它就是極小元。對於有窮集合B極小元一定存在,但最小元不一定存在。最小元如果存在一定是唯一的,但極小元可能有多個。