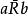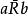偏序集

偏序集與偏序關係的概念

定義1，設P是集合，P上的二元關係“≤”滿足以下三個條件，則稱“≤”是P上的偏序關係（或部分序關係）：

（1）自反性：a≤a，∀a∈P；

（2）反對稱性：∀a，b∈P，若a≤b且b≤a，則a=b；

（3）傳遞性：∀a，b，c∈P，若a≤b且b≤c，則a≤c；

具有偏序關係的集合P為偏序集（或稱半序集），記為（P，≤）。a≤b讀作“a小於或等於b”或“a含於b”，a<b讀作“a小於b”或“a真含於b”。這裡a<b等價於a≤b且a≠b，∀a，b∈P。若a≤b或b≤a，則稱a與b是可比的，否則就說a與b是不可比。a與b不可比記作a||b。

定義2，設（P，≤）是偏序集，對於P中任意二元x，y有x≤y

yRx，則稱R是≤的逆關係，記作≤^-1。≤^-1稱為≤的逆。

定理1，設（P，≤）是偏序集，則（P，≤^-1）也是偏序集，偏序集（P，≤^-1）稱為偏序集（P，≤）的對偶，簡記作P^-1。

定義3，設（P，≤）是偏序集，N

P，由於關係≤是P×P的子集，令≤_N=≤∩(N×N)是≤與N×N的交集，則稱≤_N是關係≤在N上的限制。

定理2，設（P，≤）是偏序集，關係≤_N是≤在N上的限制，則（N，≤_N）是偏序集，稱為（P，≤）的子偏序集。

刻畫偏序關係的一種示意圖。即有限集A的偏序結構<A，R>的直觀圖示。圖中用小圓圈表示集合A的元素。在a,b∈A，aRb時，從a有一條連續上升的不必筆直的線段或折線到達b。下面各圖都可以看成集合的哈塞圖。設R是集合A的偏序關係，則在偏序結構<A,R>的哈塞圖中：

1、aRb，若且唯若a到b有一條或幾條嚴格上升的線段或折線連結。a與b間無線連結，或雖有折線連結但在上下起伏的時候，

且

。如圖1中

，

等（

為R的補關係）。

2、無水平的線段。

3、當R是全序時，哈塞圖可畫成一個上升的鏈狀圖，如圖4。

4、同一個集合，當偏序關係不同時，有不同的哈塞圖。例如，當A={2,3,4,6,8}時，關係R=“x不大於y”，G=“x整除y”時，R與G的哈塞圖分別為圖5與圖6。

5、集合A的兩個哈塞圖相同，若且唯若通過變形可以把一個變成另一個，但是必須不改變圖的連線並保持線段的上升方向。例如，圖6、圖7是同一個哈塞圖。

6、把一個關係的哈塞圖上下反轉，得到它的逆關係的哈塞圖，但左右翻轉還是原關係的哈塞圖。