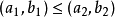在數學中,一個集合具有某種意義上的有限的大小,則稱這個集合在這種意義下是有界的,否則,稱為無界的。
定義,度量空間,序理論中的有界性,例,
定義


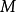



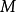
歐氏空間 的一個集合
的一個集合 ,如果有實數
,如果有實數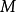 ,使得
,使得 中的所有點
中的所有點 ,都有
,都有 。則該集合為有界的。
。則該集合為有界的。


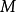



度量空間
度量空間 的子集
的子集 是有界的,如果它包含在有限半徑的球中,即存在
是有界的,如果它包含在有限半徑的球中,即存在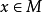 和
和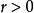 ,使得對任意的
,使得對任意的 ,有
,有 。
。 稱為有界度量空間 ,如果M作為其自身的子集是有界的。
稱為有界度量空間 ,如果M作為其自身的子集是有界的。


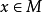
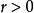



- 完全有界意味著有界。對於歐氏空間的子集, 兩者是等價的。
- 度量空間是緊的當僅當它是完備的且完全有界的。
- 歐氏空間的子集是緊的當僅當它是有界閉集。
序理論中的有界性
實數的子集是有界的,如果存在一個上界和一個下限。此定義可擴展到任何偏序集的子集。須要注意, 這個更一般的有界概念並不對應於 "數的大小" 的概念,而是一種順序的前後。
偏序集 的子集
的子集 稱為有上界的,如果存在元素
稱為有上界的,如果存在元素 ,使得對任意
,使得對任意 ,有
,有 。
。 稱之為
稱之為 的一個上界。類似地,可以定義有下界的。若子集既有上界同時有下界,則稱為有界的。
的一個上界。類似地,可以定義有下界的。若子集既有上界同時有下界,則稱為有界的。







例
對歐氏空間 中的
中的 ,定義偏序
,定義偏序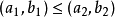 當僅當a1≤a2且b1≤b2,此時,歐氏空間的子集有界性等價於在剛才定義偏序集的有界性。類似地,可推廣到
當僅當a1≤a2且b1≤b2,此時,歐氏空間的子集有界性等價於在剛才定義偏序集的有界性。類似地,可推廣到 。
。