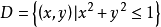無界集

無界集(unbounded set)即非有界集，若E⊆Rⁿ，則E無界意味著對任意M>0，存在x∈E，使得|x|>M，或者說，E的直徑為+∞，對實數集E來說，E無界還意味著E沒有上界或沒有下界，若E⊂R沒有上界(下界)，即sup E=+∞(inf E=-∞)，則存在E中不同的點組成的點列{a_n}，使a_n→+∞(-∞)；反之也成立。有窮集必是有界集，因此，無界集必是無窮集。

基本介紹

• 中文名：無界集
• 外文名：unbounded set
• 所屬學科：數學
• 相關概念：有界集，開、閉集，有界閉區域等

基本介紹

對於平麵點集E，如果存在某一個數r，使得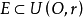，其中為坐標原點，則稱E為有界集，否則稱為無界集。例如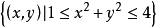，為有界閉區域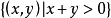，為無界開區域。

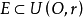
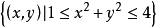
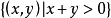
一般地，稱點集E內兩點問最大距離為該點集的直徑。若點集E的直徑是有限值，稱E為有界點集，否則稱為無界點集。

註：(1)閉區域雖然包含有邊界，但它也有可能是無界的；開區域是不含有邊界的，但它也可能為有界域。

(2)開區域一定是開集，閉區域一定是閉集，而開集未必是開區域，閉集未必是閉區域。

基本介紹

點集

一個二元有序數組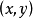對應於平面內一個點，這種點的集合稱為平麵點集。三元有序數組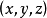的點集就稱為空間點集。

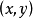
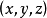
例如，平麵點集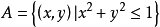表示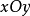坐標平面上，以半徑為1的圓的內部且包括圓周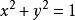(圖1中陰影部分)。

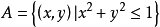
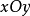
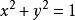
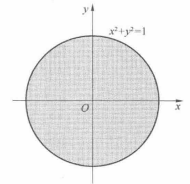圖1

區域(開區域)

區域分為平面區域和空間區域。平面區域是指平面上由一條或幾條曲線圍成的部分，而空間區域指空間上由一個或幾個曲面圍成的部分。連通的開集稱為開區域，簡稱為區域。例如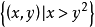，就是一區域。

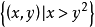
鄰域

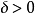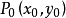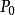設，在平面上給定一個點，則以為圓心、以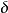為半徑的圓區域

稱為點的鄰域，記為。有時，在討論問題時，若不需要強調鄰域的半徑，點的鄰域可簡記為。

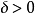
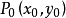
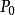
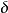
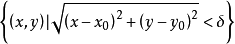
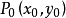
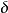
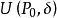
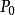
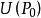
內點

設E為平面上的一個點集，如果點P屬於E，且存在點P的某個鄰域，使這鄰域中的所有點都屬於E，則稱P為E的內點(圖2中點)。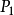

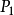
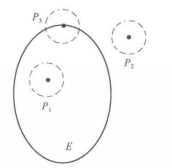圖2

外點

如果存在點P的某個鄰域U(P)，使得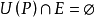，則稱P為E的外點(圖2中點)。

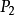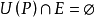
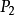
邊界點

若點P的任一鄰域內既含有屬於E的點，又含有不屬於E的點，則稱點P為E的邊界點(圖2中點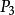)。E的邊界點的全體稱為邊界，通常記作。

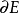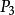
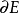
開集

如果點集E的點都是E的內點，則稱E為開集。例如，點集

中每個點都是的內點，故為開集。

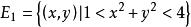
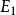
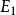
閉集

開集連同它的邊界構成的點集稱為閉集。例如，集合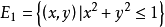就是一閉集。

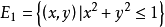
連通集

如果點集D內任意兩點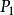和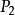，都可以用折線將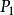和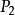連線起來，且折線上的點都在D內，則稱D為連通集。

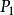
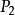
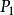
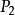
閉區域

開區域連同它的邊界一起所構成的點集稱為閉區域。例如，點集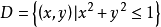就是一閉區域。