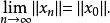點列

點列(range of points)是射影幾何的基本概念之一，指一條直線上所有點的集合。該直線稱為點列的底。收斂點列一定是基本點列，但基本點列不一定有極限。由點列強收斂可推出其弱收斂。

基本介紹

• 中文名：點列
• 外文名：range of points)
• 概述：一條直線上所有點的集合
• 符號表示：l(A,B,C,...)
• 領域：射影幾何
• 學科：數學

定義

點列(range of points)是射影幾何的基本概念之一，指一條直線上所有點的集合。該直線稱為點列的底，以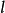 為底，以點A,B,C,…為元素的點列記為

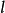
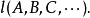
基本點列

設（x，ρ）是距離空間，{x_n}是X中的點列，如果對任意正數ε，存在自然數N，使得m，n≥N時，

則稱{x_n}是X中的基本點列；如果X中任何基本點列都收斂於X中的點，則稱X為完備的距離空間。

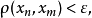
註：收斂點列一定是基本點列，但基本點列不一定有極限。

點列的收斂性

弱收斂:設X為賦范線性空間，x_n，x∈X，若對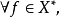 有

則稱{x_n}弱收斂於x，記作w-

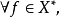
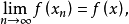
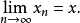
強收斂：設X為賦范線性空間，x_n，x∈X，當

時，稱{x_n}強收斂於x，記作s-

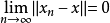
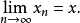
註：1.由點列強收斂可推出其弱收斂。[1]

證明：由

可證。並且強極限存在時必等於其弱極限，反之卻不然。

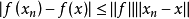
2.設X為賦范線性空間，x_n，x∈X，則w-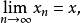 若且唯若

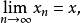
（1）

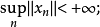
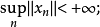
（2）存在X*上一個稠密集Y，使得

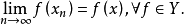
3.設X為一致凸的賦范線性空間，則X中的點列{x_n}強收斂於x₀的充要條件是{x_n}弱收斂於x₀，且有