設X是非空集合,對於X中任意的兩個元素x與y,按某一法則都對應唯一的實數d(x,y),而且滿足下述三條公理:
(1)(非負性)d(x,y)≥0[d(x,y)=0,若且唯若x=y];
(2)(對稱性)d(x,y)=d(y,x);
(3)(三角不等式)對於任意的x,y,z∈X,恆有d(x,y)≤d(x,z)+d(z,y)。
則稱d(x,y)為x與y的距離,並稱X是以d為距離的距離空間,記作(X,d)。通常,在距離已被定義的情況下,(X,d)可以簡單地將X中的元素稱為X中的點。
基本介紹
- 中文名:距離空間
- 外文名:metric space
- 所屬學科:數學
- 所屬領域:泛函分析
- 別名:度量空間
- 性質:是一種拓撲空間
定義
點集
開球

閉球




球面




內點





開集

閉集


鄰域
聚點
導集
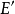
閉包
孤立點

























