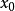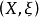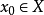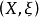極限點

極限點是點列的收斂子列的極限，a是R_e中的點列{a_e}的極限點的充分必要條件是a的任何鄰域內有{a_e}的無窮多項，或等價地，對任意正整數e₀，在a的任何鄰域內都有{a_e}的下標≥e₀的項，點列可以有一個或多個極限點，也可以沒有極限點。若且唯若只有一個極限點時點列收斂，每個有界點列至少有一個極限點。對實數列，為了便於處理某些問題，也把定向發散子列的極限(即±∞)算作極限點，這樣，實數列的極限點就是它的收斂子列或定向發散子列的極限。根據收斂子列原理，實數列{a_e}有上(下)界若且唯若{a_e}的所有極限點的集合L有上(下)界，並且sup L∈L，inf L∈L，即sup L與inf L也是{a_e}的極限點，因而是L的最大元與最小元(可以是+∞或-∞)。在文獻中，聚點與極限點這兩個名稱的使用是混亂的，許多人把數集的聚點稱為極限點，也有一些書籍把數列的極限點稱為數列的聚點。

基本介紹

• 中文名：極限點
• 外文名：limit point
• 所屬學科：數理科學
• 相關概念：極限、拓撲空間、數列、點列等

關於極限

在點集拓撲學中也有與極限相似的概念，叫做極限點。從字面上看，極限點是極限就要到達的那一點。有時所說極限是數列或函式的極限，是變動的數的極限，極限過程是變數。有時所說極限是點列或映象的極限，是變動的點的極限，極限過程是動點。

度量空間點列

定義1

設 是度量空間 的無限點列，a是常數，不管給定的正數 多么小，總存在N>0，當 ， ，則稱a是無限點列 的一個極限點。

定義2

設 是度量空間 的無限點列，a是 的一個極限點。則稱無限點列 收斂於a或極限為a，記為 。

例1 無限恆常數列 的極限點或極限均是x。

例2設 是離散拓撲空問， ，任意x∈X， 是含x的開球，若要點列 收斂於x，則含x的開球必須包含 幾乎所有的項，之後的項均為X，從而 。

註記1：度量空間點列的極限點或極限是唯一的，但在非度量拓撲空間中，極限點或極限就不一定唯一。請看例3。

例3設 是平凡拓撲空間，任意點x∈X，若 是X中的點列，則因為 中只有一個非空集X，所以包含x的球只有X，從而點列 收斂於X的任一點x。

極限點的定義

定義3

設 是拓撲空間，，若對每個

中的集合B，s∈B，有

則稱s是A的一個極限點。

註記2：定義3是在非度量拓撲空間中極限點的定義，它比定義1和定義2更廣泛，一般不具唯一性。

定理1

設X是非空集，

是平凡拓撲．即 ，則以下3個結論成立：

(1)若A是空集，則A無極限點；

(2)若A是單點集，其元素為 ，則只要 ，x都是A的極限點；

(3)若A至少有2個元素，則A中每一點都是A的極限點。

雙核拓撲會計

在雙核拓撲會計空間中所有的點都不是極限點，原因是以下定理。

定理2

設 是離散拓撲空間， 。則 不可能是任何 的極限點。

定理3

雙核拓撲會計空間資產核 中，若 ，則所有資產核綱目都不存在極限點。

證明 是X的所有子集的系，即 ，由定理2，任何 不可能是任何綱目 的極限點。

定理4

雙核拓撲會計空間權益核 中，若 ，則所有權益核綱目都不存在極限點。

證明 同定理3的證明。

註記3：雙核拓撲會計空間Z沒有極限點，是因為我們為雙核會計空間選用了離散拓撲結構，由定理2．任何在單點集 中的點x都不可能是任何Z中的子集的極限點。

註記4：若我們為雙核會計空間選用平凡拓撲結構，則由定理1，空間每一點都是至少有兩個元素的集合的極限點，但是平凡拓撲結構太粗，不適合雙核會計空間。