基本介紹
- 中文名:聚點
- 外文名:cluster point、accumulation point
- 所屬學科:拓撲學
- 提出者:康托爾
基本介紹
定義
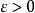

聚點與極限
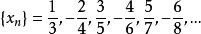


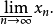
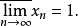
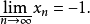
聚點存在定理
定理1

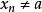


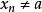



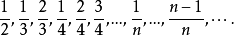
定理2
定理3
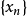


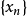
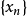
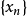
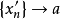
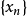

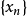

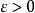

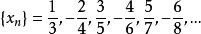


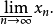
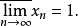
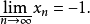

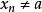


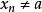



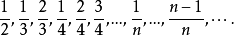
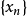


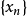
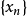
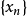
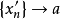
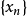

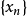
聚點是拓撲空間的基本概念之一。設A為拓撲空間X的子集,a∈X,若a的任意鄰域都含有異於a的A中的點,則稱a是A的聚點。集合A的所有聚點的集合稱為A的導集,...
聚點原理(accumulative point principle)亦稱外爾斯特拉斯定理,或波爾查諾-外爾斯特拉斯定理,刻畫實數系R的連續性的常用命題之一。它斷言:R(Rn或度量空間)的每個有界...
完全聚點(complete accumulation point)是一類特殊的聚點。設A為拓撲空間X的子集,x∈A。若對於x的任意鄰域U有|U∩A|=|A|,則稱x為A的完全聚點,其中|A|表示...
聚點均衡是指多個納什均衡間不存在帕雷托占優關係或明顯的風險占優關係,如夫妻愛好問題的兩個純策略均衡。...
聚點工作室是由一群熱愛文字的青少年組成。該工作室有最強悍的宣傳團隊,有最廣泛的人脈關係。不僅與網路推廣公司強強聯手,並且還成立了自己的宣傳小組。凡是經過該...
聚點定理,也稱為維爾斯特拉斯聚點定理,定量內容是:實軸上的任一有界無限點集S至少有一個聚點。該定理的一般形式(又叫緻密性定理,波爾查諾-維爾斯特拉斯定理)...
聚點翻轉成立於2007年9月,樂團曲風獨立搖滾(融入了R&B說唱等元素);樂團宗旨:將每一股血液都化成搖滾的音符!為夢而轉,無堅不摧!JDFZ SHOW TIME...
浙江聚點科技有限公司於2010年11月09日在溫州市鹿城區工商行政管理局登記成立。法定代表人陳鋒,公司經營範圍包括一般經營項目:開發、銷售計算機網路套用軟體等。...
北京聚點互聯科技有限公司於2015年11月25日成立。法定代表人牛福明,公司經營範圍包括:技術推廣服務;軟體開發;計算機系統服務;企業策劃;設計、製作、代理、發布廣告;...
北京聚點時尚文化傳媒有限公司,簡稱“聚點傳媒”,是一家以多媒體互動娛樂為核心,以藝人的包裝、推廣、培養、輸出為業務的新生網際網路文化傳媒機構。聚點傳媒成立於2016...
聚點串吧是一家餐館,位於北京市東城區鼓樓外大街60號。...... 北京聚點餐飲有限責任公司成立於2005年3月,公司成立至今,一直傾力打造屬於北京的燒烤品牌--"聚點串 ...
四川聚點人力資源服務有限公司於2014年07月28日成立。法定代表人靳清泉,公司經營範圍包括:收集、儲存、發布人才供求信息和提供諮詢服務;人才推薦和代理招聘;人才信息...
聚點電商是一家阿里系人創建的專業的紅人電商技術服務公司,目前已簽約眾多紅人,總部位於杭州市。 聚點電商的主要經營內容有紅人電商孵化,品牌電商運營,淘寶直播,天貓...
深圳市聚點數碼科技有限公司成立於2010年,是一家以“追求卓越,不斷創新,專業真誠,服務客戶”為宗旨的三維動畫影視技術公司。 聚點數碼專注於製作影視動畫、電子售樓...
北京聚點互動科技有限公司於2013年05月17日在朝陽分局登記成立。法定代表人王強,公司經營範圍包括技術推廣服務;經濟貿易諮詢;設計、製作、代理等。...
北京聚點餐飲有限責任公司成立於2005年3月,公司成立至今,一直傾力打造屬於北京的燒烤品牌——“聚點串吧”,聚點串吧——以經營精品特色燒烤、麻辣涮肚與北京獨家吊...
聚點燒烤位於河東區中山門東里七段13號樓底墒,是一家以燒烤為主的店。近來店裡有些冷清。等串的時候,老闆攀談:生意不好做!經濟危機著實厲害!連周末,食客也不...
聚點快遞社區編輯 鎖定 以快遞服務為主,並提供其他綜合的社區服務,覆蓋全國70多家物業社區。中文名 聚點快遞社區 [1] 是成都源禾豐創科技有限公司旗下的社區品牌,...
聚點網公司致力於幫助企業最大限度地提高廣告效率、增加廣告效果、減少廣告風險。...... 聚點網公司致力於幫助企業最大限度地提高廣告效率、增加廣告效果、減少廣告風險...
華為聚點廣告平台已於2012年8月1日正式上線運營,聚點廣告平台由華為公司自主研發,也是華為移動廣告業務重拳打造的國內領先的智慧型廣告平台。華為移動廣告業務成立於2004...
北京聚點餐飲有限責任公司成立於2005年3月,公司成立至今,一直傾力打造屬於北京的燒烤品牌——“聚點串 吧”,聚點串吧——以經營精品特色燒烤、麻辣涮肚與北京獨家吊...
聚點傳媒公司成立於2008年初,以經營城市電視聯播系統為主。...... 聚點傳媒公司成立於2008年初,以經營城市電視聯播系統為主。公司名稱 聚點傳媒 成立時間 2008年初...
北京今視聚點文化傳媒有限公司於2014年04月16日成立。法定代表人許斌,公司經營範圍包括:企業文化藝術交流活動(不含演出);設計、製作、代理、發布廣告;企業管理諮詢;...
企業簡介福州聚點網路公司成立於2013年(原名聚點網路工作室)是一家專業為中小型企業開發網站,服務範圍包括企業網站策劃建設、廣告設計及企業宣傳推廣等相關服務。 主力...
新聚點(廣州)網路科技有限公司於2017年11月15日成立。法定代表人樊躍來,公司經營範圍包括:計算機批發;計算機零售;計算機零配件零售;計算機技術開發、技術服務;計算機...
深圳聚點互動科技有限公司是一家專注於無線音頻套用平台開發的公司,致力於推動智慧型音箱行業的發展,引領智慧型家居新生活。 公司在內容集成,後台推送,網路互聯等多方面有...
(2)分為聚點、孤立點、外點。內點外點 外點,即如果存在點P的某個鄰域U(P),使得U(P)∩E=Φ,則稱P為E的外點。 [2] ...
