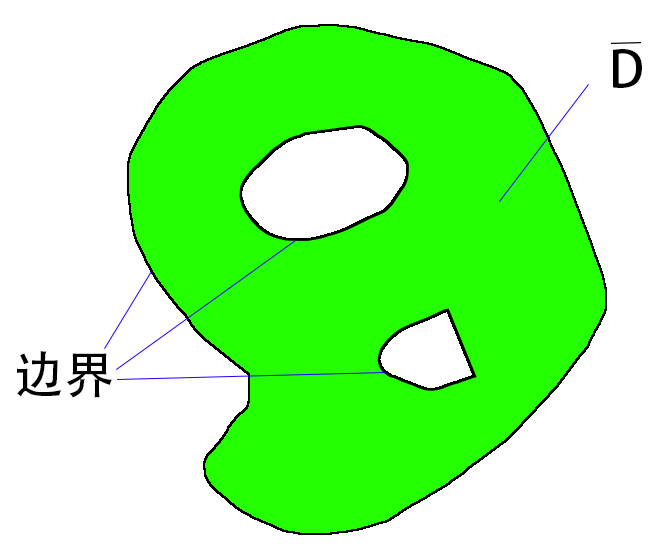
閉區域(closed region)是指簡單閉曲線及它的內部,構成“平面閉區域”。類似地,可定義空間閉區域。也稱區域與它的邊界的並集稱為閉區域。區域(region)是幾何學的基本概念之一,如果一個平面圖形(封閉圖形,不包含其內部)能將平面上不屬於圖形上的點分為若干個部分,使得同一部分任意兩點可以用一條與圖形無公共點的折線連結,不同部分的任意兩點不能用與圖形無公共點的折線連結,那么這個平面的每個部分都稱為一個區域,該圖形稱為區域的邊界。如果某一個區域的任意兩點可以用與該圖形無公共點的線段連結,那么這個區域稱為凸區域。例如,一直線分平面為兩個凸區域,兩相交直線分平面為四個凸區域,三角形分平面為兩個區域,其中只有一個凸區域(三角形的內部)。一個區域連同它的邊界稱為閉區域。
基本介紹
- 中文名:閉區域
- 外文名:Closed Region
- 所屬學科:數學(幾何學)
- 相關概念:區域、連通、開集、開區域等
定義
定義1
定義2



相關概念
平麵點集
鄰域
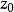

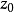
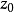
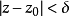



開集
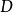

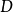
連通

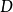

區域的定義

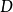


簡單曲線與閉曲線






單連域與多連域
常見的區域
區域 | 不等式 |
圓域 |  |
角形域 | 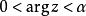 |
帶形域 |   |
圓環域 | 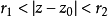 (復連通域) |