基本介紹
定義
區間


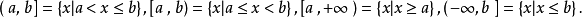








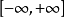
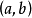

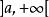
閉區間套定理
閉區間套


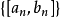
定理
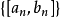

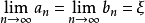



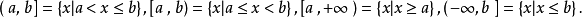








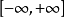
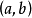

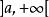


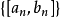
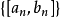

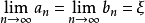
閉區間是數學用語,與開區間相對。 閉區間是直線上的連通的閉集,是直線上介於固定兩點間的所有點的集合(包括給定的兩點),用[a,b]來表示(包含兩個端點a和b)(...
在數學裡,區間通常是指這樣的一類實數集合:如果x和y是兩個在集合里的數,那么,任何x和y之間的數也屬於該集合。例如,由符合0 ≤ x ≤ 1的實數所構成的集合,...
閉區間套定理:如果{[an,bn]}形成一個閉區間套,則在實數系中存在唯一的實數ξ屬於所有的閉區間[an,bn],n=1,2,3,…;即an≤ξ≤bn , n=1,2,3,…。...
區間數就是用區間表示的數,它實際上是一個閉區間上所有實數所組成的集合,其運算法則一般與集合的運算法則類似。...
n維區間是一種特殊點集,是R中區間概念的推廣。設(ai,bi),[ai,bi](i=1,2,…,n;ai,bi∈R*)是R*中的區間,積集∏i=1n(ai,bi)與∏i=1n[ai,bi],...
閉區域(closed region)是指簡單閉曲線及它的內部,構成“平面閉區域”。類似地,可定義空間閉區域。也稱區域與它的邊界的並集稱為閉區域。區域(region)是幾何學的...
介值定理,又名中間值定理,是閉區間上連續函式的性質之一,閉區間連續函式的重要性質之一。在數學分析中,介值定理表明,如果定義域為[a,b]的連續函式f,也就是說...
4.半開半閉區間、無限閉區間都不是R中的開集半開半閉的區間(a,b]={x∈R|a<x≤b},[a,b)={x∈R|a≤x...
閉區間上的連續函式具有一些重要的性質,是數學分析的基礎,也是實數理論在函式中的直接體現。下面的性質都基於f(x)是[a,b]上的連續函式得出的結論。...
效率可能比較低下:二是區間等長劃分長度的確定,既要滿足線路上運行的動車組的性能要求,又不能太長以影響運行效率,需要調整閉塞分區的劃分方式以達到效率和經濟的...
包含在特定要求範圍內的所有數值的集合被稱作取值範圍。一旦區間分配給某個對象(表、索引及簇),則該區間就不能再分配給其它對象。...
由於鐵路車輛的制動距離較汽車長得多(以高鐵最明顯),當列車運行途中發現前方線路有危險狀況時,大多數情況下都是來不及停車的,所以將鐵道分為一個個區塊(閉塞區間...
但這裡有一個很微妙的問題,即與連續性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
有限覆蓋定理:設H是閉區間[a,b]的一個(無限)開覆蓋,則必可以從H中選擇有限個開區間來覆蓋[a,b]。有限覆蓋定理是一個有用而且重要的定理.它是數學分析處理...
函式極限的存在性、可微性,以及中值定理、積分等問題,都是與函式的連續性有著一定聯繫的,而閉區間上連續函式的性質也顯得非常重要。在閉區間上連續函式的性質中,...
如果函式y= f(x)在區間[a,b]上的圖象是連續不斷的一條曲線,並且有f(a)·f(b)<0,那么,函式y= f(x)在區間(a,b)內有零點,即存在c∈(a,b),使得f...
