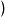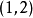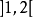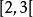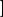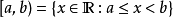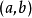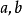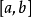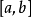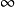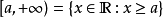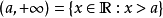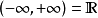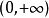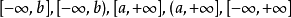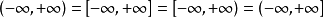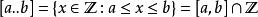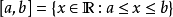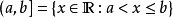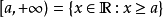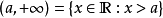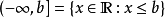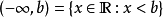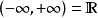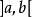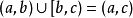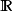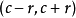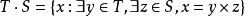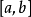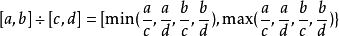在數學裡，區間通常是指這樣的一類實數集合：如果x和y是兩個在集合里的數，那么，任何x和y之間的數也屬於該集合。例如，由符合0 ≤ x ≤ 1的實數所構成的集合，便是一個區間，它包含了0、1，還有0和1之間的全體實數。其他例子包括：實數集，負實數組成的集合等。
區間在積分理論中起著重要作用，因為它們作為最"簡單"的實數集合，可以輕易地給它們定義"長度"、或者說"測度"。然後，"測度"的概念可以拓，引申出博雷爾測度，以及勒貝格測度。
區間也是區間算術的核心概念。區間算術是一種數值分析方法，用於計算捨去誤差。
區間的概念還可以推廣到任何全序集T的子集S，使得若x和y均屬於S，且x<z<y，則z亦屬於S。例如整數區間[-1...2]即是指{-1,0,1,2}這個集合。
基本介紹
- 中文名：區間
- 外文名：interval
- 類型：數學概念
- 記號：()和[]
- 地位：區間算術的核心概念
- 標準：新制訂的ISO 80000-2
- 套用範圍：數學領域
記號,定義,無限區間,分類,區間表示法,性質,定義推廣,區間算術,
記號
通用的區間記號中，圓括弧表示“排除”，方括弧表示“包括”。例如，區間(10, 20)表示所有在10和20之間的實數，但不包括10或20。另一方面，[10, 20]表示所有在10和20之間的實數，以及10和20。而當我們任意指一個區間時，一般以大寫字母 I 記之。
有的國家是用逗號來代表小數點，為免產生混淆，分隔兩數的逗號要用分號來代替。例如[1, 2.3]就要寫成[1; 2,3]。否則，若只把小數點寫成逗號，之前的例子就會變成 [1,2,3] 了。這時就不能知道究竟是 1.2 與 3 之間，還是 1 與 2.3 之間的區間了。
在法國及其他一些歐洲國家，是用
與
代替
與
。比如
寫成
，
寫成
。這種寫法原先也包括在國際標準化組織編制的ISO 31-11內。ISO 31-11是一套有關物理科學及科技中所使用的數學符號的規範。在2009年，已由新制訂的ISO 80000-2所取替，不再包括 與 的用法。
定義
用集合的語言，我們定義各種區間為：
注意
均是代表空集，單元素集合不能用區間表示，如集合{0}不能表示為[0]或[0,0]。而當a>b時，上述的四種記號一般都視為代表空集。區間不為空集時，a, b稱為區間的端點。一般定義 b - a 為區間的長度。區間的中點則為 (a+b)/2。
區間[a,b]有時也稱為線段。（不為空集或單元素集的話）
除了表示區間，圓括弧和方括弧也有其他用法，視乎語境而定。譬如
也可表示集合論中的有序對丶解析幾何中點的坐標，線性代數中向量的坐標，有時也用來表示一個複數，有時在數論中，用
表示整數
的最大公約數。
也偶爾用作表示有序對，尤其在計算機科學的範疇里。同樣在數論里，用
表示整數
的最低公倍數。
無限區間
我們可以用
符號來表示區間在某方向上無界。具體定義如下：
特別地，
表示正實數集，亦記作
。
則表示了非負實數集。
一般使用的便是以上五種記號，而
等的寫法則相當少見。有的作者假定區間為實數集的子集，對於他們來說，這些寫法要麽是無意義，要麽就是跟用圓括弧的意思沒兩樣。在後者的情況下，我們可以寫作
。於是實數集可被視為又開又閉的區間。
如果我們考慮擴展的實數軸，那么這四種寫法是有數的區間。
一般而言，對於整數a,b，具體寫作：
。
除了[a..b]，也有{a..b}和a..b的寫法，意思一樣。
如果一個整數區間是有界的話，那麽它必然包含最小數a和最大數b。因此，如果想定義去掉最小數或最大數的區間，只需用[a..b-1], [a+1..b]或[a+1..b-1]表示。無需像實數區間般引進 [a..b)或(a..b)的記號。
分類
實數區間一共可分成11種，如下所列。其中a,b是實數，且a<b。
1. 空集：
2.退化區間 (degenrate interval)：
有界區間
3. 閉區間：
4. 開區間：
5. 左閉右開區間：
6. 左開右閉區間：
單側無界
7. 左閉：
8. 左開：
有上界但無下界：
9. 右閉：
10. 右開：
11. 雙側無界：
#1、#4、#8、#10、和#11可稱為“開區間”（標準拓撲下是開集），#1、#2、#3、#7、#9和#11可稱為“閉區間”（標準拓撲下是閉集）。#3和#4有時稱為“半開區間”或“半閉區間”。#1和#11同時為“開”和“閉”，並非“半開”、“半閉”。
區間表示法
性質
定義推廣
多維區間
n=2時，一般來說是定義了一個長方形，它的長和闊分別平行於兩條坐標軸。n=3時，一般的是定義了一個長方體，它的各邊同樣是平行於坐標軸。
複數區間
複數的區間可定義成複平面上的一個區域，兩種合理的選擇是長方形或圓盤。
