區間分析,又稱區間數學,是一門用區間變數代替點變數進行運算的數學分支。它最初是從計算數學的誤差理論研究發展起來的。1966年R.E.穆爾在《區間分析》一書中第一次系統提出區間運算理論。
基本介紹
- 中文名:區間分析
- 外文名:Interval analysis
- 別稱:區間數學
- 提出者:R.E穆爾
- 提出時間:1996年
- 套用學科:數學,統計學
區間分析的產生
概念

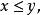

區間分析,又稱區間數學,是一門用區間變數代替點變數進行運算的數學分支。它最初是從計算數學的誤差理論研究發展起來的。1966年R.E.穆爾在《區間分析》一書中第一次系統提出區間運算理論。

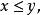
區間分析,又稱區間數學,是一門用區間變數代替點變數進行運算的數學分支。它最初是從計算數學的誤差理論研究發展起來的。1966年R.E.穆爾在《區間分析》一書中第一...
在數學裡,區間通常是指這樣的一類實數集合:如果x和y是兩個在集合里的數,那么,任何x和y之間的數也屬於該集合。例如,由符合0 ≤ x ≤ 1的實數所構成的集合,...
預測區間即預先推測或測定任何的連續塊,除了點預測外還有另外一類預測問題,即區間預測。預測區間則是通過預測方法得到的目標的取值區間。預測是指在掌握現有信息的...
區間計算曾主要套用於計算誤差控制領域。近年來,區間計算在處理不確定性方面的優點被重新認識並在許多新領域裡得到了套用。...
置信區間是指由樣本統計量所構造的總體參數的估計區間。在統計學中,一個機率樣本的置信區間(Confidence interval)是對這個樣本的某個總體參數的區間估計。置信區間...
《角度·區間-股票價格波動》是2007年中國科學技術出版社出版的圖書,作者是王建。本書介紹了利用區間分析方法利用它進行分析,可以將莊家各種走勢區間的性質進行準確...
《角度·區間》是2007年中國科技出版社出版的圖書。作者是王建。...... 利用區間分析方法是一種非常有效的分析方法,利用它進行分析,可以將莊家各種走勢區間的性質進...
"區間信號系統"是鐵路部門為了保證列車在車站與車站之間的“區間”運行時的絕對安全所必須的技術裝備,也稱自動閉塞。...
n維區間是一種特殊點集,是R中區間概念的推廣。設(ai,bi),[ai,bi](i=1,2,…,n;ai,bi∈R*)是R*中的區間,積集∏i=1n(ai,bi)與∏i=1n[ai,bi],...
區間交易指一段時間內某種金融工具在市場上所創出的最高價和最低價,英文常稱為hi/lo(高點/低點)。技術分析師很重視價格是否突破先前建立的區間交易,因為突破區間...
區間參數結構的靜動態分析,論文,楊曉偉著,陳塑寰教授指導。...... 區間參數結構的靜動態分析,論文,楊曉偉著,陳塑寰教授指導。副題名外文題名Dynamic and static analy...
數據流分析是一項編譯時使用的技術,它能從程式代碼中收集程式的語義信息,井通過代數的方法在編譯時確定變數的定義和使用。...
包含在特定要求範圍內的所有數值的集合被稱作取值範圍。一旦區間分配給某個對象(表、索引及簇),則該區間就不能再分配給其它對象。...
