區間計算曾主要套用於計算誤差控制領域。近年來,區間計算在處理不確定性方面的優點被重新認識並在許多新領域裡得到了套用。
基本介紹
- 中文名:區間計算
- 外文名:interval computing
- 套用:計量經濟分析
- 發展:30年代
- 作者:R.E.Moore
- 套用:誤差控制
基本介紹
套用


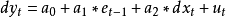

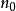






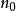
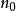


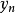
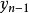



區間計算曾主要套用於計算誤差控制領域。近年來,區間計算在處理不確定性方面的優點被重新認識並在許多新領域裡得到了套用。


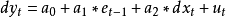

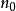






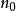
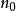


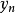
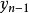


區間計算曾主要套用於計算誤差控制領域。近年來,區間計算在處理不確定性方面的優點被重新認識並在許多新領域裡得到了套用。...
在數學裡,區間通常是指這樣的一類實數集合:如果x和y是兩個在集合里的數,那么,任何x和y之間的數也屬於該集合。例如,由符合0 ≤ x ≤ 1的實數所構成的集合,...
區間分析,又稱區間數學,是一門用區間變數代替點變數進行運算的數學分支。它最初是從計算數學的誤差理論研究發展起來的。1966年R.E.穆爾在《區間分析》一書中第一...
區間數就是用區間表示的數,它實際上是一個閉區間上所有實數所組成的集合,其運算法則一般與集合的運算法則類似。...
置信區間是指由樣本統計量所構造的總體參數的估計區間。在統計學中,一個機率樣本的置信區間(Confidence interval)是對這個樣本的某個總體參數的區間估計。置信區間...
區間估計(interval estimate)是在點估計的基礎上,給出總體參數估計的一個區間範圍,該區間通常由樣本統計量加減估計誤差得到。與點估計不同,進行區間估計時,根據樣本...
預測區間即預先推測或測定任何的連續塊,除了點預測外還有另外一類預測問題,即區間預測。預測區間則是通過預測方法得到的目標的取值區間。預測是指在掌握現有信息的...
區間測速是在同一路段上布設兩個相鄰的監控點,原理是基於車輛通過前後兩個監控點的時間來計算車輛在該路段上的平均行駛速度,並依據該路段上的限速標準判定車輛是否...
區間消去法(interval elimination method)是求單變數函式無約束極值的較實用的一類直接搜尋方法,其特點是在搜尋過程中,不斷縮小最優點所在的區間,即通過搜尋區間的...
按一定的機率或可信度(1-α)用一個區間來估計總體參數所在的範圍,該範圍通常稱為參數的可信區間或者置信區間(confidence interval,CI),預先給定的機率(1-α)稱為...
點估計和區間估計是抽樣推斷的兩種方法。點估計是在抽樣推斷中不考慮抽樣誤差,直接以抽樣指標代替全體指標的一種推斷方法。因為個別樣本的抽樣指標不等於全體指標,所以...
區間通過能力是指在一定的機車車輛類型、信號設備和行車組織方法條件下,鐵路區段內各項固定設備在單位時間內(通常為一晝夜)所能通過的最大列車數。固定設備包括區間...
貝葉斯區間估計比經典的區間估計更容易處理,因為參數是隨機變數,對給定置信度1-α,利用θ的後驗分布可以較方便地求得θ的置信區間。...
所謂閉塞,就是保證區間或閉塞分區在同一時間內只能運行一個列車,而保證一個區間或閉塞分區在同一時間內只能運行一個列車的設備稱為閉塞設備。閉塞是鐵路上防止列車...
區間震盪線(DPO),是由惠特曼·巴塞特(Walt Bressert)提出的。是一個排除價格趨勢的震盪指標。它試圖通過扣除前期移動平均價來消除長期趨勢對價格波動的干擾,從而便於...
5 置信區間 6 計算 t分布歷史 編輯 在機率論和統計學中,學生t-分布(Student's t-distribution)經常套用在對呈常態分配的總體的均值進行估計。它是對兩個樣本均...
