區間消去法(interval elimination method)是求單變數函式無約束極值的較實用的一類直接搜尋方法,其特點是在搜尋過程中,不斷縮小最優點所在的區間,即通過搜尋區間的逐步縮小來確定最優點。
基本介紹
- 中文名:區間消去法
- 外文名:interval elimination method
- 所屬學科:數學(非線性規劃)
- 簡介:通過區間的逐步縮小確定最優點
基本介紹
區間消去法原理










 圖1(a)
圖1(a)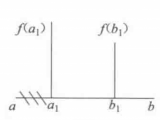 圖1(b)
圖1(b)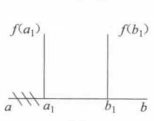 圖1(c)
圖1(c)















區間消去法(interval elimination method)是求單變數函式無約束極值的較實用的一類直接搜尋方法,其特點是在搜尋過程中,不斷縮小最優點所在的區間,即通過搜尋區間的逐步縮小來確定最優點。










 圖1(a)
圖1(a) 圖1(b)
圖1(b) 圖1(c)
圖1(c)














區間消去法(interval elimination method)是求單變數函式無約束極值的較實用的一類直接搜尋方法,其特點是在搜尋過程中,不斷縮小最優點所在的區間,即通過搜尋區間的...
斐波那契法(Fibonacci method),又稱Fibonacci法、斐波那契分數法,是一種一維搜尋的區間消去法。這種方法與0.618法(黃金分割法)類似,也是用於單峰函式,在計算過程中,...
性能指標比較複雜或不能用變數顯函式表示時,可以採用直接搜尋法,經過若干次疊代搜尋到最優點,數值計算法可以分為兩大類:(1)區間消去法,又稱為一維搜尋法,適用於...
搜尋區間確定之後,採用區間消去法逐步縮短搜尋區間,找到極小點的數值近似解。假定在搜尋區間內[a,b] 任取兩點 、 ,且 , 。1.若 ,新區間為 ;...
性能指標比較複雜或不能用變數顯函式表示時,可以採用直接搜尋法,經過若干次疊代搜尋到最優點,數值計算法可以分為兩大類:(1)區間消去法,又稱為一維搜尋法,適用於...
近似黃金分割法(approximate golden sectionmethod)一種區間消去法(參見“區間消去法”).利用近似黃金分割數進行一維搜尋的方法.因為黃金分割數。是無理數,實用中取...
性能指標比較複雜或不能用變數顯函式表示時,可以採用直接搜尋法,經過若干次疊代搜尋到最優點,數值計算法可以分為兩大類:(1)區間消去法,又稱為一維搜尋法,適用於...
性能指標比較複雜或不能用變數顯函式表示時,可以採用直接搜尋法,經過若干次疊代搜尋到最優點,數值計算法可以分為兩大類:(1)區間消去法,又稱為一維搜尋法,適用於...
7 1 2區間消去法——菲波那西法和黃金分割法1617 1 3插值法1737 2無約束多變數函式最最佳化的單純形法1787 2 1方法概述1787 2 2程式框圖1817 2 3計算實例...
最優控制系統數值法 若性能指標較為複雜,無法用解析式表達,則可通過數值分析的方法,通過疊代搜尋找到最優點 [3] 。一般可分為區間消去法(一維)和爬山法(多維)...
3.5.4黃金分割法的流程圖3.5.5黃金分割法的MATLAB程式3.5.6實例測試3.6三點二次插值法3.6.1三點二次插值法的原理3.6.2四種不同的區間消去情況3.6.3三點二次...
5 1 2搜尋最優區間715 2黃金分割法72 [1] 5 2 1區間消去法的基本原理725 2 2黃金分割法的特點和步驟725 2 3典型套用舉例74...
§4.3區間消去類最佳化方法45§4.3.1黃金分割法基本原理46§4.3.2黃金分割法疊代過程和程式流程圖46§4.3.3斐波納契數法48§4.3.4平分法48§4.4插值類最佳化方法49...
3.1概述3.2搜尋區間的確定與區間消去法原理3.3一維搜尋的試探方法3.4一維搜尋的插值方法思考題第4章無約束最佳化方法4.1概述4.2最速下降法...
第二節 搜尋區間的確定與區間消去法原理 56 第三節 一維搜尋的試探方法 59 第四節 一維搜尋的插值方法 62 第四章 無約束最佳化方法 67 第一節 概述 68 第二...
(1)區間消去法,又稱為一維搜尋法,適用於求解單變數極值問題。主要有黃金分割法、多項式插值法等。(2)爬山法,又稱多維搜尋法,適用於求解多變數極值問題。主要有...
3.2.2一維搜尋的區間消去方法323.2.3黃金分割法323.2.4二次插值法323.2.5牛頓法333.3典型例題333.4習題393.5習題參考答案40...
7.1.2區間消去法――菲波那西法和黃金分割法 7.1.3插值法 7.2無約束多變數函式最最佳化的單純形法 7.2.1方法概述 7.2.2程式框圖 7.2.3計算實例...
