基本介紹
- 中文名:勒貝格測度
- 外文名:Lebesgue measure
- 提出時間:1902年
- 領域:數理科學
歷史
例子
性質
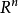
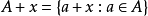
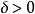
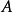
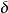
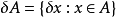
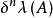
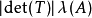
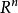
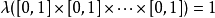
零測集

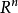
勒貝格測度的結構
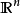
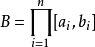
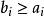
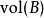
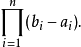
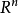
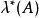
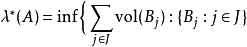
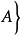
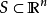
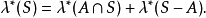
與其他測度的關係
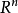
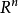
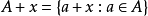
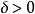
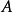
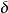
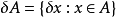
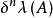
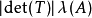
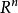
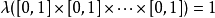

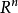
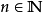
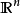
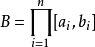
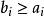
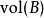
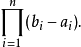
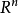
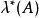
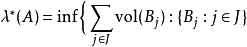
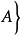
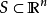
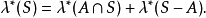
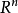
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;...
勒貝格積分,是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是求其函式圖像與軸之間的面積。...
測度論是研究一般集合上的測度和積分的理論。它是勒貝格測度和勒貝格積分理論的進一步抽象和發展,又稱為抽象測度論或抽象積分論,是現代分析數學中重要工具之一。 ...
取R的全體子集作為F,設其σ域F',F'包括所有的區間,而且其中的元素都有測度L,且L是區間長度概念的自然推廣,可得到勒貝格測度空間(R,F',L),F'中的元素叫...
零測度就是某個集合的測度為0。數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。...
勒貝格內測度是勒貝格(Lebesgue,H.L.)提出他的測度定義時所用的一個輔助性概念,簡稱(L)內測度。...
勒貝格一斯蒂爾傑斯測度簡稱(L-S)測度,是直線上勒貝格測度的推廣。...... 勒貝格一斯蒂爾傑斯測度簡稱(L-S)測度,是直線上勒貝格測度的推廣。設g(x)是定義在R上...
拉東測度是一種正則測度。抽象測度的簡稱,即非負可列可加的集函式,測度論研究的對象。拉東在變分法、實變函式、泛函分析、微分幾何、相對論的數學理論等方面都有...
機率測度(probability measure)是機率論、遍歷理論等數學分支中常用的一種重要的有限測度。在數學中,機率測度是在滿足測度屬性(如可加性)的機率空間中的一組事件上...
度量空間是弗雷歇(Fréchet,M.-R.)於1906年引進的,它是現代數學中的一種基本而重要並且非常接近於歐幾里得空間的抽象空間,也是泛函分析的基礎之一。勒貝格數(...
《機率與測度》是2007年世界圖書出版公司出版的圖書,作者是別林斯里。該書主要內容包括機率、測度、積分、隨機變數及數學期望、分布的收斂的問題、導數與條件期望、...
勒貝格積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是函式...
測度完備化(completion of a measure)亦稱測度完全化,是由任一測度延拓成的完備測度。...
數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的,後來人們希望把積分...
δ測度是測度論中的一個概念。給定一個δ-代數 ,以及其上的一個測度 ,如果該測度是一個有限的實數(而不是無窮大),那么就稱這個測度為有限測度。如果 能夠表示...
