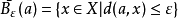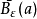基本介紹
- 中文名:勒貝格數
- 外文名:Lebesgue number
- 領域:數學
- 空間:緊度量空間
- 相關概念:覆蓋
- 提出人物:勒貝格
概念,覆蓋,度量空間,開球,人物簡介——勒貝格,
概念
勒貝格數(Lebesgue number)是緊度量空間中與覆蓋有關的數。若X是緊度量空間,B是X的任意開覆蓋,則存在正數λ使得{Bλ(x)|x∈X}是B的加細,其中Bλ(x)為度量空間X中以x為中心λ為半徑的開球。正數λ稱為覆蓋B的勒貝格數。上述結論稱為勒貝格覆蓋定理。
覆蓋
數學的一個重要概念。這裡指一類節點子集。具體地說,圖的一個節點子集使該圖的每一條邊都與這個子集中一個節點關聯,稱這樣的節點子集為覆蓋集,也稱點覆蓋集,簡稱覆蓋。圖G的最小覆蓋,也稱最小點覆蓋,是指在圖的所有覆蓋中,節點數最少的覆蓋。G的最小覆蓋的節點數稱為G的覆蓋數,或點覆蓋數,常記為β(G)。一個圖稱為覆蓋臨界圖,或點覆蓋臨界圖,若從這圖上去掉任何一條邊後,所得的圖的覆蓋數都小於原圖的覆蓋數。設有一個最小覆蓋M,若對於它的任何一個子集M′,與M′中節點相鄰的不在M中的節點的數目總不比M′的節點數少,則稱M為一個外部最小覆蓋或外最小點覆蓋。不是任何一圖都有外最小覆蓋。事實上,一個圖有外最小覆蓋若且唯若它有一個點核,或邊核。
拓撲空間的基本概念。一種特殊的集族。設A是由集合組成的族。若它的所有成員的並包含集合B,則稱該集族A是B的一個覆蓋,或稱A覆蓋B。在拓撲空間X中,若A的每一成員都是X的開集(或閉集),並且A覆蓋X,則稱A是X的開覆蓋(或閉覆蓋)。若A的子族A1也是B的覆蓋,則稱A1是A的子覆蓋。當覆蓋A為有限集或可數集時分別稱A為有限覆蓋或可數覆蓋。
度量空間
度量空間亦稱距離空間。一種拓撲空間,其上的拓撲由距離決定。設R是一個非空集合,ρ(x,y)是R上的二元函式,滿足如下條件:
1.ρ(x,y)≥0且ρ(x,y)=0⇔x=y;
2.ρ(x,y)=ρ(y,x);
3.(三角不等式)ρ(x,y)≤ρ(x,z)+ρ(y,z);
則稱ρ(x,y)為兩點x,y之間的距離,R按距離ρ成為度量空間或距離空間,記為(R,ρ)。設A是R的子集,則A按R中的距離ρ也成為度量空間,稱為R的(度量)子空間。如果把上述距離的條件1改為ρ(x,y)≥0且ρ(x,x)=0,則稱ρ為R上的擬距離。當ρ(x,y)=0時,記x~y。~是R上的一個等價關係,記商集(即等價類全體)為D=R/~,在D上作二元函式ρ~:ρ~(x~,y~)=ρ(x,y)(x∈x~,y∈y~),則ρ~是D上的距離,而(D,ρ~)稱為R按擬距離ρ導出的商(度量)空間。
度量空間(R,ρ)中的子集A稱為有界的,如果對x0∈R,存在常數M,使ρ(x0,x)≤M對A中的一切x成立。設x0∈R,r>0,則稱集合{x|x∈R,ρ(x,x0)<r}為以x0為中心,r為半徑的開球,或x0的r鄰域,記為O(x0,r)。又設A⊂R,若對任何x∈A,存在x的某個鄰域O(x,r)⊂A,則A稱為開集;而稱開集的補集為閉集。R中包含子集A的最小閉集就稱為A的閉包。
開球
度量空間的基本概念之一。設(X,d)為度量空間,a∈X,ε為正數。令:
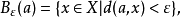
人物簡介——勒貝格
法國數學家。生於博韋(Beauvais),卒於巴黎。1894—1897年學於巴黎高等師範學校,是波萊爾(Borel)的學生。在雷恩(Rennes)及普瓦捷(Poitiers)大學取得學位。後任巴黎大學教授。1921年起任法蘭西學院教授,被選為法國科學院院士。他是“勒貝格積分”理論的創始人。他的博士論文《積分、長度、面積》(Integr-ale,longueur,aire,1902)改進了波萊爾的測度理論。建立了“勒貝格測度”、“勒貝格積分”的概念。這是現代積分論的開端,也是傅立葉級數理論和位勢論發展的轉折點。勒貝格在《積分與原函式的研究》(Lecons sur l'integration et larecherche des fonctions primitives,1904)中證明了有界函式黎曼可積的充要條件是不連續點構成一個零測度集。這完全解決了黎曼可積性的問題。在拓撲學方面,他引入了緊性定義及緊度量空間的勒貝格數。勒貝格晚年致力於數學教育及初等幾何的研究,例如在《幾何作圖問題》(Lecons sur les constructionsgeometriques)中討論了幾何的尺規作圖問題。