若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。
基本介紹
- 中文名:有界
- 外文名:bounded
- 所屬領域:數學
- 相關概念:上界、下界、無界等
定義
定義1
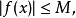
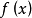
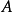
定義2

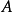
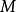
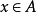
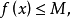

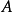

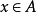
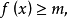

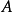

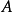




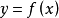
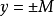
 圖1
圖1注意點
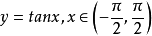
 圖2
圖2例題解析
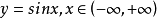
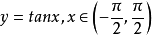

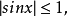
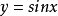
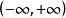
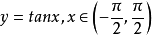
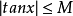
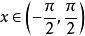
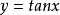
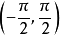
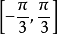
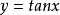
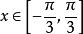
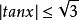
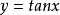
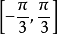
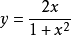
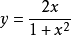
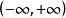
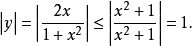
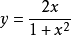
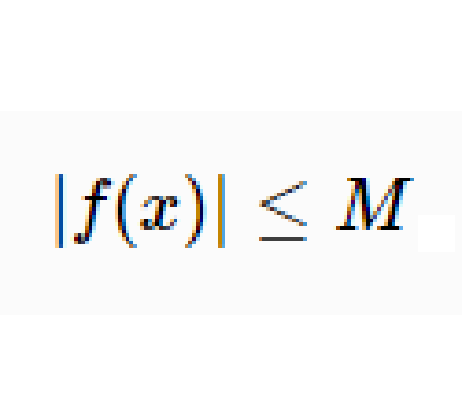
若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。
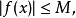
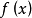
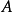

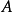
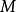
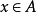
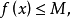

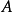

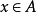
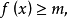

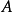

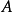




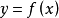
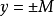
 圖1
圖1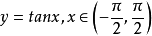
 圖2
圖2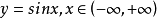
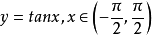

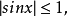
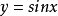
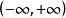
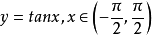
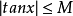
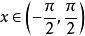
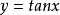
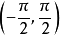
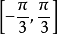
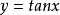
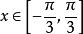
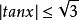
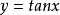
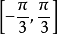
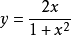
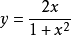
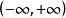
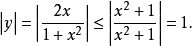
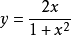
若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。...
有界集(bounded set)是一類重要的集合,指可以被有界區間包含的實數集,也就是被長度有限的區間包含的集合。“有界”和“邊界”是不同的概念,後者看到邊界(拓撲)...
有界列是一種特殊的序列。對於數列{xn},若存在實數M(m),使對所有n∈N,有xn≤M(xn≥m),則稱{xn}有上(下)界。既有上界又有下界的數列稱為有界數列,...
在極限理論中,我們知道閉區間上連續函式具有5個性質,即:有界性定理、最大值與最小值定理、介值定理、零點定理和一致連續性定理。其中,零點定理是介值定理的一個...
有界函式是設f(x)是區間E上的函式,若對於任意的x屬於E,存在常數m、M,使得m≤f(x)≤M,則稱f(x)是區間E上的有界函式。其中m稱為f(x)在區間E上的下界...
設有映射f:D⊂X→Y,若對於D中的每個有界集S,f(S)為Y中的有界集,則稱f:D→Y為有界映射。...
有界控制(bounded control)值域屬於歐氏空間中的有界集合的控制函式.記r維歐氏空間R”中的集合U是系統的控制域.稱定義在時間區間「to ,t}]上的控制函式u(t)...
有界格是具有最大元與最小元的格,通常以0,1分別記最小元與最大元.有限個元素a1,a2,…,an所構成的格是有界格,其最小元是a1·a2·…·an,最大元是a1+...
有界完全統計量(boundedly complete statistic)是常用的一類完全統計量,設(X,BX,P)是一個統計結構,其中P={Pθ:θ∈Θ},如果對於BX可測的有界函式φ(X),由...
任一項的絕對值都小於等於某一正數的數列。有界數列是指數列中的每一項均不超過一個固定的區間,其中分上界和下界。假設存在定值a,任意n有{An(n為下角標,下同...
有界度量空間拓撲空間 編輯 度量空間具有許多良好性質,例如,它滿足第一可數公理,它是豪斯多夫空間,正規空間,還是仿緊空間。此外對度量空間而言,緊緻性等價於下列三...
本性有界函式類又稱L空間,是在一個零集之外有界的函式的全體。這樣函式的全體稱為E上的本性有界函式類,記為L∞(E)或L∞。...
一致有界性是指一個函式族中的函式有共同的界。一致有界的函式族中每個函式均有界,反之不然。...
函式的有界性是數學術語。設函式f(x)的定義域為D,f(x)在集合D上有定義。如果存在數K1,使得 f(x)≤K1對任意x∈D都成立,則稱函式f(x)在D上有上界。反...
齊性有界域是一類重要的有界域。齊性域D若為有界域,則稱為齊性有界域。...... 齊性有界域是一類重要的有界域。齊性域D若為有界域,則稱為齊性有界域...
泛函分析中一種重要的運算元。運算元(映射)有線性和非線性之分.線性運算元又分為有界和無界兩類,有界線性運算元是線性賦范空問的基本概念。...
局部有界空間是一類拓撲線性空間,如果拓撲線性空間E中存在零元的一個有界的鄰域,則稱E是局部有界的。局部有界空間是亥爾斯(D.H.Hyers)於1939年引入的,局部有...
在數學中,一個集合具有某種意義上的有限的大小,則稱這個集合在這種意義下是有界的,否則,稱為無界的。...
定義:設函式f(x)的定義域為R.若存在與x無關的正常數M,使 |f(X) |≤M|x|對一切實數x均成立,則稱f(x)為有界泛函. 舉例 f(x)=(sinx+cosx)x ...
函式的有界性定義:若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。...
《Cn中的齊性有界域理論》是2000年科學出版社出版的圖書,作者是許以超。...... 《Cn中的齊性有界域理論》是2000年科學出版社出版的圖書,作者是許以超。...
對稱有界域是研究得最深入的一類齊性有界域。Cn中的域稱為對稱有界域,如果它關於伯格曼度量為對稱埃爾米特流形。對稱有界域為齊性有界域,它雙全純同構於不可...
全有界一致空間 ( totally bounded uniformspace)亦稱準緊一致空間.設(X,)為一致空間.若X的任意一致覆蓋都有有限子覆蓋,則稱(X,0u)為全有界一致空間.( X,...
確界原理( supremum and infimum principle )是刻畫實數完備性的命題之一。設S為非空數集。若S有上界,則S必有上確界;若S有下界,則S必有下確界。...
