有界列是一種特殊的序列。對於數列{xn},若存在實數M(m),使對所有n∈N,有xn≤M(xn≥m),則稱{xn}有上(下)界。既有上界又有下界的數列稱為有界數列,簡稱有界列。
基本介紹
- 中文名:有界列
- 外文名:bounded sequence
- 適用範圍:數理科學
簡介
性質
推廣
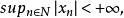
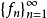
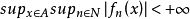
有界列是一種特殊的序列。對於數列{xn},若存在實數M(m),使對所有n∈N,有xn≤M(xn≥m),則稱{xn}有上(下)界。既有上界又有下界的數列稱為有界數列,簡稱有界列。
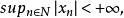
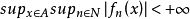
有界列是一種特殊的序列。對於數列{xn},若存在實數M(m),使對所有n∈N,有xn≤M(xn≥m),則稱{xn}有上(下)界。既有上界又有下界的數列稱為有界數列,...
有界數列,是數學領域的定理,是指任一項的絕對值都小於等於某一正數的數列。有界數列是指數列中的每一項均不超過一個固定的區間,其中分上界和下界。假設存在定值...
無界列是非有界的序列,有無窮極限的數列必無界,反之不一定,但無界的單調數列必有無窮極限。...
(2)若存在N>0,n>N時,對n都滿足|xn|≦M,M>0,則稱數列{x}為有界數列,否則則稱為無界數列無界數列舉例 編輯 有界數列:1,2,3,4 無界數列:1,2,3,4...
若{ an}、{ bn}都是無窮小列,{ an+bn},{ an-bn}也是無窮小列。若{ an}是無窮小列,{bn}是有界數列,則{ anbn}也是無窮小列。...
數列極限的問題作為微積分的基礎概念,其建立與產生對微積分的理論有著重要的意義...緻密性定理 任何有界數列必有收斂的子列。數列極限套用 編輯 (1)求極限 [2]...
依據緻密性定理,有界數列必有收斂子列,收斂子列的極限中的最大者與最小者特別重要,這就是數列的上、下極限的概念。...
的值都可以表示為一個有理數序列的極限,但當x為有理數時,這個值卻是無理數。柯西序列其他性質 任何收斂數列必然是柯西列,任何柯西列必然是有界序列。如果...
1、唯一性:若數列的極限存在,則極限值是唯一的,且它的任何子列的極限與原數列的相等。 2、有界性:如果一個數列’收斂‘(有極限),那么這個數列一定有界。 但...
聚點定理,也稱為維爾斯特拉斯聚點定理,定量內容是:實軸上的任一有界無限點集S至少有一個聚點。該定理的一般形式(又叫緻密性定理,波爾查諾-維爾斯特拉斯定理)...
在數學分析中,巴拿赫極限(英語:Banach limit)指的是定義在全體有界復序列組成的巴拿赫空間上,對每個巴拿赫空間中的序列和複數滿足一定條件的連續線性泛函。...
R中的任何基本列都在R中收斂。稱滿足公理組I的集為域;滿足公理組I與II的集...但這裡有一個很微妙的問題,即與連續性公理等價的7個實數系的基本定理(確界...
1、唯一性:若數列的極限存在,則極限值是唯一的,且它的任何子列的極限與原數列的相等。2、有界性:如果一個數列’收斂‘(有極限),那么這個數列一定有界。...
首先數列的定義是:按一定次序排列的一列數稱為數列(sequence of number)。數列...按照有界性分為有界數列和無界數列。 一個數列每一項的絕對值都小於某個正數(...
(維爾斯特拉斯聚點定理)任何有界的無窮數集,都有聚點存在。 [3] 聚點定理3 (波爾察諾定理) 有界數列有收斂的子數列。證明若數列 有無窮多項相同,它們重複出現...
^n中的一個子集E是序列緊緻(每個序列都有收斂子序列)若且唯若E是有界閉集...都包含一個收斂的子列,其極限也是K中元素,就稱K具有波爾查諾-魏爾斯特拉斯性質...
波爾查諾-維爾斯特拉斯定理是指有界數列必有收斂子列。從極限點的角度來敘述緻密性定理,就是:有界數列必有極限點。...
區間套定理與單調有界定理、數列的緻密性定理和柯西收斂準則、聚點定理、有限覆蓋定理共同構成實數集完備性的基本定理,並且這六個定理是相互等價的,對於研究實數集的...
再利用數學歸納法可以證明數列有上界,事實上 ,設 ,那么 。根據單調有界數列必收斂,可設 ,且必有 ,從而由 可得 ,得唯一正數解 ,即 。...
