基本介紹
- 中文名:外爾斯特拉斯定理
- 外文名:Bolzano–Weierstrass theorem
歷史
定理
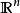
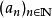
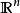
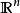
波爾查諾-魏爾斯特拉斯性質
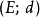
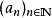
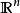
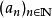
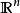
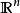
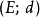
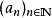
外爾斯特拉斯定理,即波爾查諾-魏爾施特拉斯定理,是數學拓撲學與實分析中用以刻劃R^n中的緊集的基本定理,得名於數學家伯納德·波爾查諾與卡爾·魏爾施特拉斯...
外爾斯特拉斯-斯通定理是函式逼近論中的基本定理。外爾斯特拉斯定理是關於實變函式逼近的定理,它本身包含兩個結論:外爾斯特拉斯第一定理和外爾斯特拉斯第二定理。它們是...
林德曼-外爾斯特拉斯定理(Lindemann-Weier-strass theorem)伽羅瓦理論的一條重要定理.由林德曼(Lindemann, (C. L. )F. von)提出,經外爾斯特拉斯(Weierstrass, (K....
外爾斯特拉斯空隙定理稱:設R為虧格g>0的閉黎曼曲面,p∈R為任一點,則存在且僅存在g個整數 ,使得不存在R上的亞純函式,它在R\{p}上為全純,而以p點ni級...
外爾斯特拉斯逼近定理證明 編輯 第一逼近定理可以從第二逼近定理直接推出。 [1] 第二逼近定理的證明; 設f(t)為周期為 的連續函式,定義 為一三角級數。...
波爾查諾-外爾斯特拉斯定理簡介 編輯 波爾查諾-魏爾施特拉斯定理是數學拓撲學與實分析中用以刻劃 中的緊集的基本定理,得名於數學家伯納德·波爾查諾與卡爾·魏...
斯通逼近定理是外爾斯特拉斯定理的一個重要推廣。1937年,由斯通(Stone,M.H.)建立。...... 斯通逼近定理是外爾斯特拉斯定理的一個重要推廣。1937年,由斯通(Stone,M...
解析開拓,則f(z)在D內由P(z;a)確定的分支是單值的,這便是單值性定理。...如果已知一個冪級數,它在某個有限區域內表示一個複函數,外爾斯特拉斯推導出在...
柯西的方法限於研究完全解析函式的所謂單值分支,必須通過解析開拓才能和外爾斯特拉斯的理論統一起來。阿達馬因子分解定理阿達馬 編輯 法國數學家。生於凡爾賽,卒於巴黎...
庫辛第一問題(Cousin first problem)單複變函數論中外爾斯特拉斯定理如何推廣到多復變的問題,即庫辛第一問題。...
(後來狄利克雷再次研究費馬大定理時,證明n=14時該方程無整數解。)...1870年,外爾斯特拉斯以其特有的嚴格化精神批評了狄利克雷原理在邏輯上的缺陷。...
這一定理通常稱為卡索拉蒂一外爾斯特拉斯定理。[1] 為判定線性差分方程組的基本解組,他引進了所謂卡索拉蒂行列式,其元素是某差分方程組的解,並由此給出一個...
聚點原理(accumulative point principle)亦稱外爾斯特拉斯定理,或波爾查諾-外爾斯特拉斯定理,刻畫實數系R的連續性的常用命題之一。它斷言:R(Rn或度量空間)的每個有界...
G.)定理和外爾斯特拉斯定理在多復變中的推廣的兩個問題和列維提出的擬凸域是否全純域的問題更是長期以來推動著多複變函數論的發展。...
給外爾斯特拉斯定理——解析函式可任意接近其本性奇點鄰域中的每一個值——提供了第一個完整的證明。研究了其冪級數在收斂圓周上的點發散的解析函式。論證了它們在...
外爾斯特拉斯任柏林大學教授。施瓦茲在複變函數、偏微分方程、變分學以及初等幾何等方面均有重要貢獻。最突出的工作是補救了(G.F.)B.黎曼關於映射定理證明中的缺陷...
典範乘積(canonical product)是對應於非零序列的外爾斯特拉斯基本因式構成的無窮乘積,與其相關的定理有維爾斯特拉斯定理,阿達馬定理等。...
伯恩斯坦多項式(Bernstein polynomial)逼近連續函式的一系列多項式。可在外爾斯特拉斯逼近定理的構造性證明中使用。設函式f:[0,1]→R(或C),對於n∈N+, [2] Bn(...
伯恩斯坦運算元逼近是用伯恩斯坦多項式的逼近。伯恩斯坦多項式是逼近連續函式的一系列多項式,可在外爾斯特拉斯逼近定理的構造性證明中使用。...
函式論論文集(Abhandlungen aus der Funk-tionenlehre)西方現代數學著作.德國數學家外爾斯特拉斯(Weierstrass , K. (T. W. ))著,出版於1886年.這是作者從已...
外爾斯特拉斯將多項式的因式分解定理推廣到整函式,而G.米塔-列夫勒則將有理函式分解為部分分式的定理推廣到亞純函式。(C.-)é.皮卡、(F.-é.-J.-) é....
