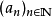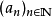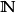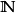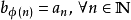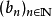基本介紹
- 中文名:波爾查諾-外爾斯特拉斯定理
- 外文名:Bolzano–Weierstrass theorem
簡介,歷史,基礎概念,波爾查諾-魏爾斯特拉斯性質,
簡介
波爾查諾-魏爾施特拉斯定理是數學拓撲學與實分析中用以刻劃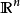 中的緊集的基本定理,得名於數學家伯納德·波爾查諾與卡爾·魏爾施特拉斯。波爾查諾-魏爾斯特拉斯定理說明,有限維實向量空間
中的緊集的基本定理,得名於數學家伯納德·波爾查諾與卡爾·魏爾施特拉斯。波爾查諾-魏爾斯特拉斯定理說明,有限維實向量空間 中的一個子集E是序列緊緻(每個序列都有收斂子序列)若且唯若E是有界閉集。
中的一個子集E是序列緊緻(每個序列都有收斂子序列)若且唯若E是有界閉集。
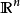

歷史
基礎概念
有界閉集: 中的有界閉集概念建立在給定的拓撲和度量上的。由於在有限維向量空間中所有度量等價,所以可以將
中的有界閉集概念建立在給定的拓撲和度量上的。由於在有限維向量空間中所有度量等價,所以可以將 視為裝備了歐幾里德度量的度量空間(並且可以定義相應的範數)。
視為裝備了歐幾里德度量的度量空間(並且可以定義相應的範數)。 的子集E有界,若且唯若所有E中元素x的範數小於一個給定常數K。注意這時對應的拓撲是歐幾里德範數誘導的自然拓撲。
的子集E有界,若且唯若所有E中元素x的範數小於一個給定常數K。注意這時對應的拓撲是歐幾里德範數誘導的自然拓撲。



序列緊緻:稱一個集合S是序列緊緻的,是指每個由集合S中元素所組成的數列都包含收斂的子列,並且該子列收斂到集合S中的某個元素。
波爾查諾-魏爾斯特拉斯性質
在有限維度量空間中,波爾查諾-魏爾斯特拉斯說明了序列緊緻的集合就是有界閉集。然而在一般的度量空間中,有界閉集不一定是序列緊緻的。為此,拓撲學中將一般度量空間中的序列緊緻稱為波爾查諾-魏爾斯特拉斯性質。
定義:
設K為度量空間 的子集。若K中任一序列
的子集。若K中任一序列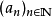 都包含一個收斂的子列,其極限也是K中元素,就稱K具有波爾查諾-魏爾斯特拉斯性質。
都包含一個收斂的子列,其極限也是K中元素,就稱K具有波爾查諾-魏爾斯特拉斯性質。