基本介紹
- 中文名:收斂
- 外文名:convergence
- 基本問題:級數的收斂發散問題
- 作用:研究函式的一個重要工具
- 套用:進行近似計算
收斂,漢語詞語,拼音:shōu liǎn,意為:1、收穫農作物。2.徵收租稅。3.聚斂;收集。4.歸總。5.檢點行為,約束身心。6.停止;消失。7.醫學用語。謂通過藥物...
數學分析的基本概念之一,它與“有確定的(或有限的)極限”同義,“收斂於……”相當於說“極限是……(確定的點或有限的數)”。在一些一般性敘述中,收斂和收斂...
收斂對於路由協定,網路上的路由器在一條路徑不能使用時必須經歷決定替代路徑的過程,是在最佳路徑的判斷上所有路由器達到一致的過程。當某個網路事件引起路由可用或不...
收斂級數(convergent series)是柯西於1821年引進的,它是指部分和序列的極限存在的級數。收斂級數分條件收斂級數和絕對收斂級數兩大類,其性質與有限和(有限項相加)...
收斂是一個經濟學、數學名詞,是研究函式的一個重要工具,是指會聚於一點,向某一值靠近。收斂類型有收斂數列、函式收斂、全局收斂、局部收斂。...
平均收斂亦稱均方收斂。...... 平均收斂編輯 鎖定 本詞條由“科普中國”百科科學詞條編寫與套用工作項目 審核。平均收斂亦稱均方收斂。中文名 平均收斂 外文名 ...
價格收斂也叫價格聚合,是指越是臨近期貨契約交割日,期貨價格越是趨近於現貨價格。是期貨市場術語。...
收斂時間是指路由器發現網路的拓撲結構發生變化後,路由信息同步的過程;而整個同步過程所共花費的時間為收斂時間,或者說是某個路由信息變化後反映到所有路由器中所...
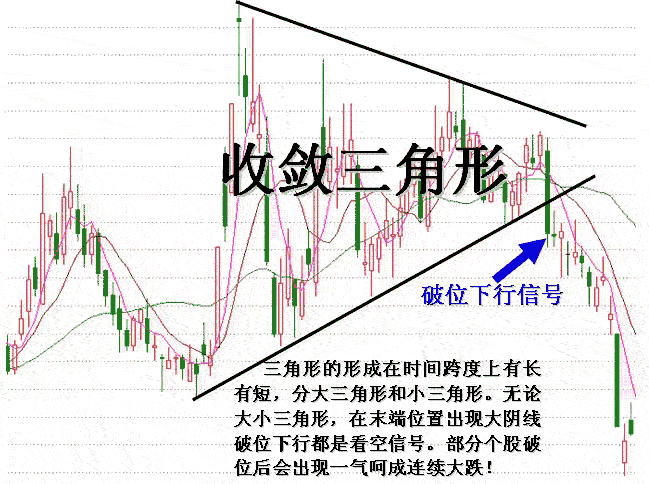
對稱三角形也叫收斂三角形,是股票比較常見的整理形態,有時也會出現趨勢逆轉突破的情況,但機率出現的比較少,通過一系列市場不完全統計,對稱三角形中大約四分之三屬...
Ras蛋白可謂多種信號傳導的匯合點,形成多條信號傳導通路的匯聚,這一特點稱為收斂作用(con-vergence)。Ras和Raf都是具有收斂作用的信號分子。[1] ...
在數值分析中, 一個收斂序列向其極限逼近的速度稱為收斂速度(Rate of convergence). 該概念多用於最最佳化算法中; 其被定義為一個疊代序列向其局部最優值逼近 (...
收斂藥(收斂劑),能沉澱組織內部分蛋白質而促使組織皺縮的藥物,有消炎退腫的作用,用於治療皮膚黏膜炎症。主要有兩類:(一)鞣酸和鞣酸蛋白。前者局部套用可治療皮膚...
設數列{Xn},如果存在常數a,對於任意給定的正數q(無論多小),總存在正整數N,使得n>N時,恆有|Xn-a|
時序收斂(英語:Timing closure)是現場可程式邏輯門陣列、專用積體電路等積體電路設計過程中,調整、修改設計,從而使得所設計的電路滿足時序要求的過程。...
收斂假說是經濟成長經驗研究的核心之一。“收斂假說”的實證檢驗,所關心的問題是:經濟是否存在新古典增長模型所預言的“穩態”和“條件收斂”,還是如內生增長理論所...
一致收斂是高等數學中的一個重要概念,又稱均勻收斂。一致收斂是一個區間(或點集)相聯繫,而不是與某單獨的點相聯繫。除了柯西準則和餘項準則外,還可以通過...
收斂形態也稱三角形,屬於整理形態,常在周曲線圖上出現,並分上、下兩種收斂形式。上收斂(多數發生在圖形的下方)時是將發生大漲的信號;下收斂(多數發生在圖形的上方...
收斂水是指較有收斂毛孔作用的化妝水, 有保濕以及收斂毛孔的功用。選擇收斂水要選酒精含量不會過多的,否則會比較刺激皮膚。...
條件收斂是一種微積分上的概念。如果級數ΣUn收斂,而Σ∣Un∣發散,則稱級數ΣUn條件收斂。...
絕對收斂一般用來描述無窮級數或無窮積分的收斂情況。如果級數ΣUn各項的絕對值所構成的級數Σ|Un|收斂,則稱級數ΣUn絕對收斂,級數ΣUn稱為絕對收斂級數。絕對收斂...
均方收斂(convergence in the mean square指的是機率論中常用的一種收斂性。...... 均方收斂(convergence in the mean square指的是機率論中常用的一種收斂性。...
收斂性質(convergence property)位勢論中的一個概念。...... 收斂性質(convergence property)位勢論中的一個概念。所謂收斂性質,是指在一定條件下單調增加的調和函式...
收斂思維(ConvergentThinking)又稱“聚合思維”、“求同思維”、“輻集思維”或“集中思維”。特點是使思維始終集中於同一方向,使思維條理化、簡明化、邏輯化、...
收斂測量是指對井巷表面兩點間的相對變形和變形規律的量測。如檢測巷道頂底板或兩幫移近量等。收斂測量系統可以分為接觸式和非接觸式兩種,接觸式主要為將多個...
