一致收斂是高等數學中的一個重要概念,又稱均勻收斂。一致收斂是一個區間(或點集)相聯繫,而不是與某單獨的點相聯繫。除了柯西準則和餘項準則外,還可以通過Weierstrass判別法、Abel判別法和Dirichlet判別法來判別函式項級數是否一致收斂。
基本介紹
- 中文名:一致收斂
- 外文名:Uniform Convergence
- 所屬學科:高等數學
- 別稱:均勻收斂
- 性質:一致收斂與一個區間相聯繫
- 判別法:Weierstrass、Abel、Dirichlet
數項級數

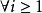







函式項級數










定義








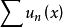

判別法


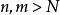
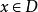




















一致收斂是高等數學中的一個重要概念,又稱均勻收斂。一致收斂是一個區間(或點集)相聯繫,而不是與某單獨的點相聯繫。除了柯西準則和餘項準則外,還可以通過Weierstrass判別法、Abel判別法和Dirichlet判別法來判別函式項級數是否一致收斂。

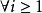

























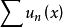



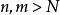
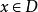



















一致收斂是高等數學中的一個重要概念,又稱均勻收斂。一致收斂是一個區間(或點集)相聯繫,而不是與某單獨的點相聯繫。除了柯西準則和餘項準則外,還可以通過...
一致收斂判別法是判定函式列與函式項級數是否收斂的重要方法,其中比較著名的有柯西準則、魏爾斯特拉斯判別法以及阿貝爾判別法等,它們是數學分析中重要的理論基礎。...
一致收斂性是函式列或函式項級數的一種性質。一致收斂函式的判別方法有很多種,最常見的有Cauchy判別法、Abel判別法、Dirichlete判別法等。一致收斂函式具有連續性、...
亦稱殆一致收斂。除外一機率任意小的事件,一致收斂的隨機變數列稱做幾乎一致收致的。 ...
近於一致收斂是一致收斂概念的推廣。設{fn(x)}為定義在可測集E上的可測函式列,對任意σ>0,若存在可測子集A⊂E,使m(A)<σ,在E\A上{fn(x)}一致...
強收斂是指測度網(或列)依範數(能量)的收斂。關於點列的收斂性包括兩種:強收斂和弱收斂,並且它們之間存在著這樣的關係:強收斂必定弱收斂,但弱收斂不一定強收斂...
已知其在一個給定的點集C上收斂得足夠快的某些多項式序列,必在一個把C包含在內的點集上收斂,這個現象就稱為過收斂。...
在數學領域拓撲學中,一致空間是帶有一致結構的集合。一致空間是帶有用來定義一致性質如完備性、一致連續和一致收斂的附加結構的拓撲空間。一致空間的概念是韋伊(Weil,...
緊收斂拓撲(topology of compact conver-gence),是映射空間上一類常見的拓撲。亦稱函式空間。拓撲學的一個基本概念。一類重要的拓撲空間。拓撲空間是歐幾里得空間的一...
Weil 引進以來,一致空間作為一種特殊的拓撲空間,能夠定義一致收斂、一致連續、完備性等一致性質的結構。一致空間與拓撲空間和度量空間存在密切的聯繫,因此一致空間成為...
在數學中,逐點收斂(或稱簡單收斂)描述的是一列函式向一個特定函式趨近的現象中的一種。簡單來說,就是對定義域裡的每一點,這個函式列在這點上的取值都趨於一...
弱收斂(weakly convergence)是一種收斂性,有點列的弱收斂、運算元列的弱收斂和泛函列的弱收斂三種情況。...
一致逼近是無窮級數的基本概念之一,指一類均勻的逼近。插值方法要求插值函式與被插函式在指定的節點處有相同的函式值及若干階相同的導數.為了提高逼近精度,可以增加...
一致柯西列是指隨著項的序號無限增大,各項的數值均勻地互相接近的函式列。...... 函式列{fn(x)}一致收斂,若且唯若它是一致柯西列(一致地滿足柯西準則)。 [1]...
數學分析的基本概念之一,它與“有確定的(或有限的)極限”同義,“收斂於……”相當於說“極限是……(確定的點或有限的數)”。在一些一般性敘述中,收斂和收斂...
收斂半徑r是一個非負的實數或無窮大,使得在 | z -a| < r時冪級數收斂,在 | z -a| > r時冪級數發散。...
積分一致絕對連續是描述測度空間中一列函式的積分絕對連續的一致性的重要概念。測度空間是定義了測度的可測空間。設(Ω,F)是可測空間,μ是F上的測度,(Ω,F,μ...
魏爾斯特拉斯判別法(Weierstrass Discriminance)是分析學中一條十分重要的判定法則,主要用於判定數項級數的收斂、函式項級數的一致收斂、反常積分的收斂以及反常含參...
阿貝爾判別法(Abel Discriminance)是分析學中一條十分重要的判定法則,與狄利克雷判別法(Dirichlet Discriminance)合稱為A-D判別法。主要用於判定數項級數的收斂、...
他的大部分時間在波倫亞工作.阿爾澤拉的主要貢獻在實變函式論方面.他引進了廣義一致收斂性的概念,給出在某區間上連續函式序列一致收斂的充分必要條件.他和阿斯科利...
魏爾斯特拉斯判別法是分析學中一條重要的判別法,主要用於判定數項級數收斂、函式項級數一致收斂以及反常積分收斂等...
在數學中,阿爾澤拉-阿斯科利定理是泛函分析中的一個定理,給出了一個從緊緻度量空間射到度量空間的函式集合是否在關於一致收斂的拓撲意義上是緊集的充分必要條件。...
