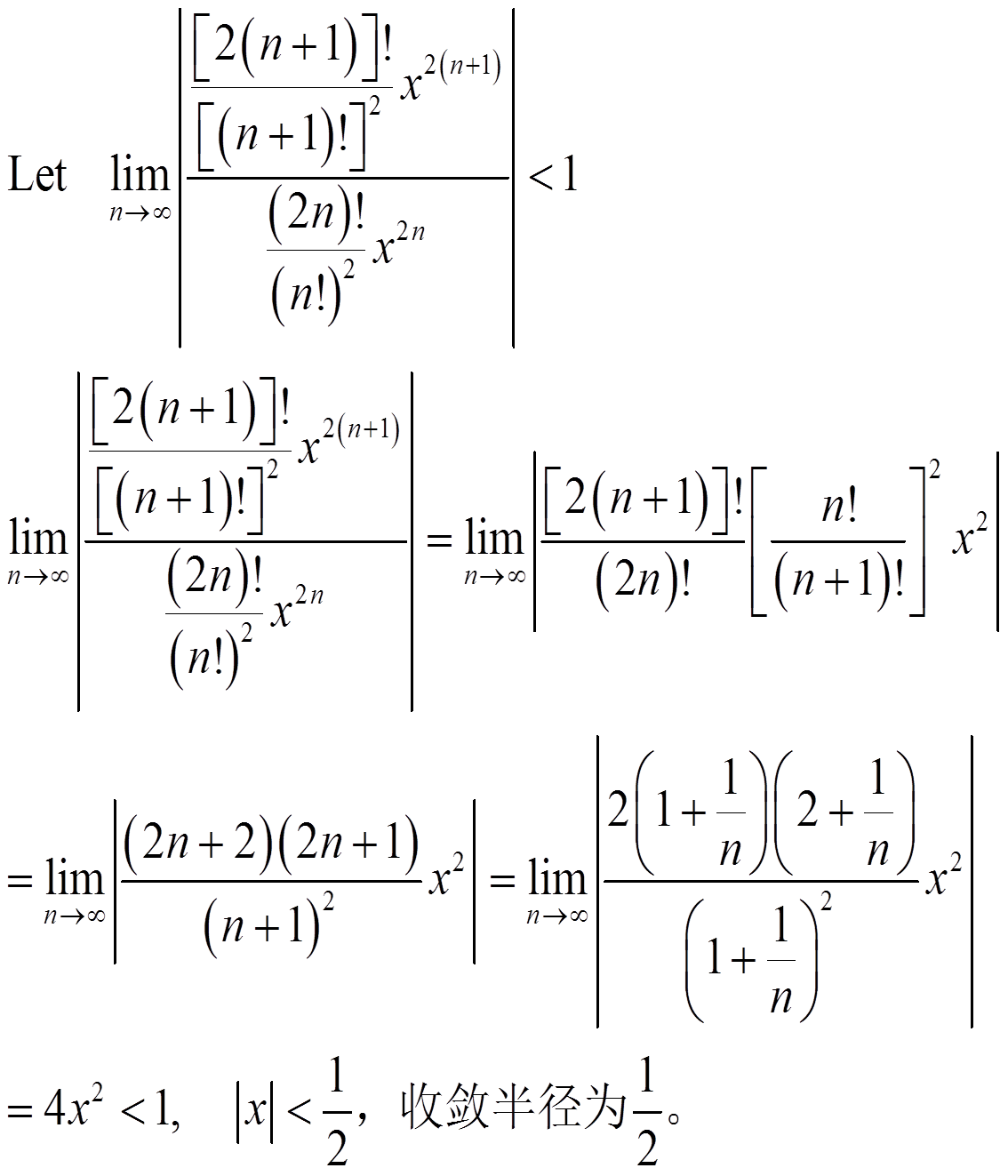收斂半徑

收斂半徑r是一個非負的實數或無窮大，使得在 | z -a| < r時冪級數收斂，在 | z -a| > r時冪級數發散。

基本介紹

• 中文名：收斂半徑
• 外文名：radius of convergence
• 屬性：非負的實數或無窮大
• 根據：達朗貝爾審斂法
• 詞性：名詞

定義

收斂半徑r是一個非負的實數或無窮大的數，使得在 | z -a| < r時冪級數收斂，在 | z -a| > r時冪級數發散。

具體來說，當 z和 a足夠接近時，冪級數就會收斂，反之則可能發散。收斂半徑就是收斂區域和發散區域的分界線。在 |z- a| = r的收斂圓上，冪級數的斂散性是不確定的：對某些 z可能收斂，對其它的則發散。如果冪級數對所有複數 z都收斂，那么說收斂半徑是無窮大。

計算

基本內容

根據達朗貝爾審斂法，收斂半徑R滿足：如果冪級數滿足，則：

是正實數時，R= ；

= 0時，R= ；

= 時，R=0。

根據根值審斂法，則有柯西-阿達馬公式。或者，複分析中的收斂半徑將一個收斂半徑是正數的冪級數的變數取為複數，就可以定義一個全純函式。

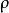
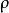
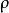
收斂半徑可以被如下定理刻畫：

一個中心為 a的冪級數 的收斂半徑 R等於 a與離 a最近的使得函式不能用冪級數方式定義的點的距離。到 a的距離嚴格小於 R的所有點組成的集合稱為收斂圓盤。最近點的取法是在整個複平面中，而不僅僅是在實軸上，即使中心和係數都是實數時也是如此。例如：函式沒有復根。它在零處的泰勒展開為：運用達朗貝爾審斂法可以得到它的收斂半徑為1。與此相應的，函式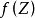 在 ±i存在奇點，其與原點0的距離是1。

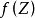
簡單例子

三角函式中的正切函式可以被表達成冪級數：

運用審斂法可以知道收斂半徑為1。

複雜例子

考慮如下冪級數展開：

其中有理數是所謂的伯努利數。對於上述冪級數，很難運用審斂法來計算收斂半徑，但運用上面提到的復域中的準則就可以很快得到結果：當 z=0 時，函式沒有奇性，因為是可去奇點。僅有的不可去奇點是其他使分母為零的取值，即使得= 0的複數 z。設，那么，要使之等於1，則虛部必須為零，於是有 ，其中 。同時得到 x= 0，回代後發現 k只能為偶數，於是使得分母為零的 z為的形式，其中 ，離原點最近距離為 ，於是收斂半徑為 。

收斂圓上的斂散性

如果冪級數在a附近可展，並且收斂半徑為 r，那么所有滿足 |z a| = r的點的集合（收斂圓盤的邊界）是一個圓，稱為收斂圓。冪級數在收斂圓上可能收斂也可能發散。即使冪級數在收斂圓上收斂，也不一定絕對收斂。

例1：冪級數的收斂半徑是 1 並在整個收斂圓上收斂。設 h(z) 是這個級數對應的函式，那么 h(z) 是例2中的 g(z) 除以 z後的導數。 h(z) 是雙對數函式。

例 2：冪級數的收斂半徑是 1 並在整個收斂圓上一致收斂，但是並不在收斂圓上絕對收斂。