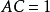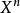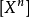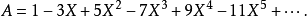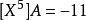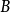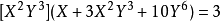基本介紹
- 中文名:柯西-阿達馬公式
- 外文名:Cauchy-Hadamard Formula
- 分類:數理科學
公式陳述,形式冪級數,
公式陳述
對於單一複數變數“z”的形式冪級數
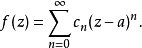
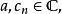
則該級數收斂半徑R 由下式給出:
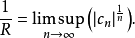
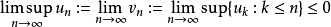
形式冪級數
形式冪級數和多項式的形式定義有類似之處。對於熟悉冪級數的讀者,也可以將其看作是不討論冪級數斂散性,也就是將其中的不定元僅僅看作是一個代數對象,而不是任何具體數值的時候寫出的冪級數。舉例來說,以下的級數式子:
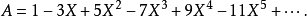
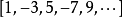
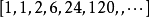
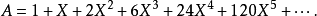
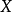
和多項式環中的元素一樣,形式冪級數之間也可以做加減和乘法的運算,具體的計算方式和多項式環一樣。比如說設:
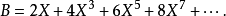
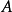
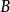
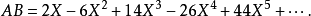
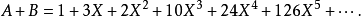
其中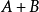 裡面
裡面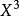 的係數就是
的係數就是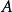 與
與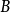 中
中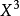 的係數的和;
的係數的和;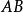 裡面
裡面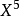 的係數就是
的係數就是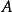 與
與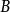 中
中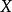 的階數相加等於5的項的係數乘積的和:
的階數相加等於5的項的係數乘積的和:
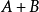
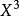
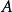
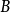
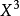
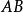
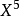
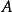
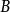
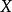
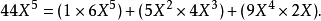

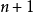
形式冪級數不僅能夠定義乘法,也能定義乘法逆的運算。一個形式冪級數 的逆是指另一個形式冪級數
的逆是指另一個形式冪級數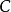 ,使得
,使得 . 如果這樣的形式冪級數
. 如果這樣的形式冪級數 存在,就是唯一的,將其記為
存在,就是唯一的,將其記為 。同時我們也可以定義形式冪級數的除法:當
。同時我們也可以定義形式冪級數的除法:當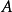 的逆存在時,
的逆存在時,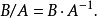 比如說,可以很容易驗證:
比如說,可以很容易驗證: